How To Find If Given Kets Form An Orthonormal Basis?
Learn about an important calculation that will help you design quantum gates and algorithms.
Now that you know most of the mathematics required for Quantum Computing, here’s an important calculation you must familiarize yourself with.
This one will help you design Quantum gates and algorithms.
Let’s begin!
In case you missed the previous lessons on the mathematics required for quantum mechanics and quantum computing, here they are:
We know that the state of a quantum system is represented by a ket vector in a complex Hilbert space.
We also know that this state is represented using a set of vectors called Orthonormal basis.
To revise:
The word “Orthonormal” means the following:
“Ortho” means that the vectors are orthogonal or perpendicular to one another
“Normal” means that the vectors are of unit length or that they have a norm of 1
For representing a quantum system in n-dimensions, the orthonormal basis will consist of a set of n unit length kets that are orthogonal to each other.
An important calculation is to find out whether a given set of kets forms an orthogonal basis or not.
Let’s learn how to do this.
Check If Two Ket Vectors Form An Orthonormal Basis
The problem goes like this:
Given two ket vectors
|a>and|b>, we need to find out if they form an Orthonormal basis.
This is easy and can be done by relying on the definition of Orthonormality and two other conditions discussed here.
Check if each ket is of unit length
This can be done by calculating the dot product of each ket with itself based on the length-finding formula.
Ket ∣a⟩ is a unit vector if:
Ket ∣b⟩ is a unit vector if:
2. Check if the kets are Orthogonal
This can be done by calculating the dot product of both kets.
The kets are orthogonal if:
And there we are!
A detailed example of this calculation can be found here.
Check If ‘N’ Ket Vectors Form An Orthonormal Basis
The problem statement is:
Given a set of
nket vectors|a>and|b>, we need to find out if they form an Orthonormal basis.
We can retake a similar approach (including the two other conditions discussed here).
For each ket, we check if it is of unit length
For each pair of kets, we check if they are orthogonal to each other
These operations can be summarized using the Kronecker delta.
For i and j representing the position of two kets in the set of n kets, the above simply means that if the dot product of:
the ket with itself (
i = j) is calculated, the result is1different kets (
i ≠ j) is calculated, the result is0
Although simple, the calculations become tedious for large n due to the number of pairwise comparisons involved.
Let’s simplify this using what we have learned in the chapter on matrix operations.
Given a set of n kets, it can be represented by a matrix A, as follows:
Next, we calculate its transpose (Hermitian transpose if the entries are complex):
Finally, we multiply them to produce a Gram matrix.
This might look complex, but it actually makes our calculations easy.
The entries on the diagonal are the squared norms of the kets.
If the kets are unit vectors, each diagonal entry will be 1.
The off-diagonal entries are the inner products of different kets.
If the kets are orthogonal, these entries will be 0.
Overall, the (A^T)(A) operation is all we need to verify if the set is an orthonormal basis.
If all its diagonal entries are 1 and non-diagonal entries are 0, the result is an Identity matrix as follows, which tells that the set of kets form an orthonormal basis.
An Example: Checking If ’N’ Ket Vectors Form An Orthonormal Basis
Let’s take a set of three kets:
The first step is to create a matrix A with these kets as its columns.
Then, we calculate the transpose of this matrix. This converts these element kets into bras.
We then calculate the product of these matrices.
This results in a 3 x 3 Identity matrix.
This confirms that the kets ∣b1⟩, ∣b2⟩, ∣b3⟩ form an orthonormal basis.
Note that the entries above and below the diagonal on the symmetrical ends are equal if the elements are real-valued.
For complex-valued elements, they are related by complex conjugation (represented by *).
Therefore, we can calculate the diagonal and either of the elements above and below in the Gram matrix, rather than both of them, saving time calculating.
That’s it for this lesson on Quantum computing.
See you soon in the next one!


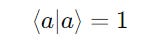
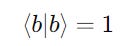
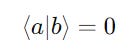
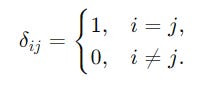
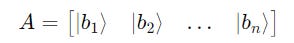
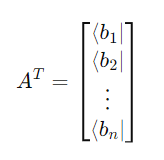
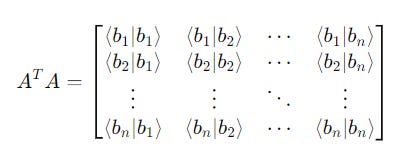
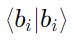
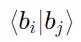
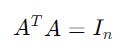
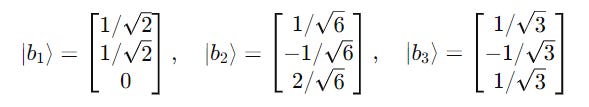
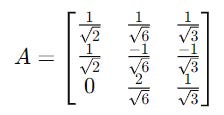
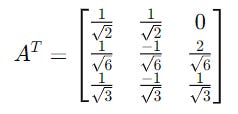
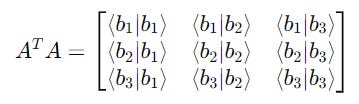
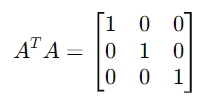
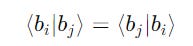
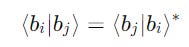

As always totally understandable and straightforward. Many thanks 🙏
I would like to discuss some weird idea of me against climate change. Would you mind to email me dirkkruggel@gmail.com ?