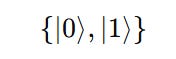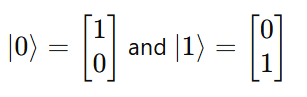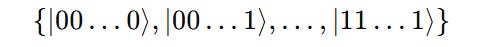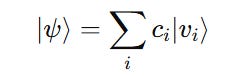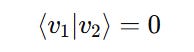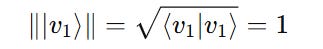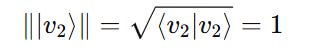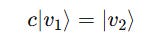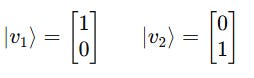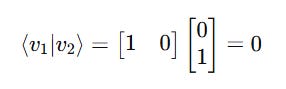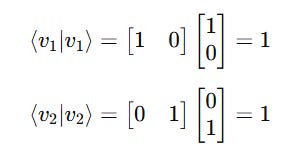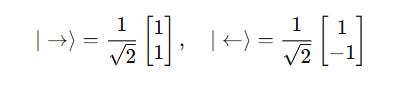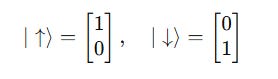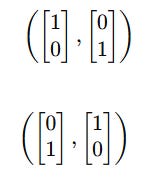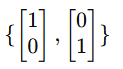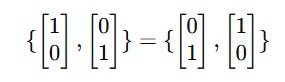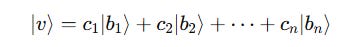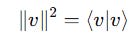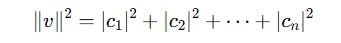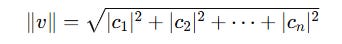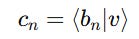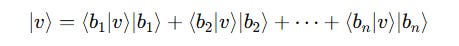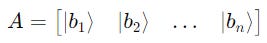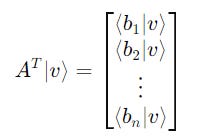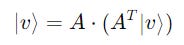An Introduction To Orthonormal Bases
An essential lesson on Orthonormal bases that help represent the state of Quantum systems.

In case you missed the previous lessons on Linear Algebra required to understand this lesson, here they are:
What’s An Orthonormal Basis?
An Orthonormal basis is a set of vectors used to represent the state of a Quantum system in a complex vector space (Hilbert Space).
The word “Orthonormal” means the following:
“Ortho” means that the vectors are orthogonal or perpendicular to one another
“Normal” means that the vectors are of unit length or that they have a norm of 1
For representing a quantum system in n-dimensions, the orthonormal basis will consist of a set of n unit kets that are orthogonal to each other.
In other words, the number of basis vectors equals the dimension of the vector space.
Note that the term ‘basis’ means a single set of vectors while ‘bases’ (pronounced “Bay-sees”) is the plural form referring to multiple such sets.
Quantum State Representation
The standard orthonormal basis for a single qubit system is given by:
where
This is called the Standard Basis.
Similarly, for a n-qubit system, the basis consists of a set of 2^n vectors.
Any quantum system (∣ψ⟩) can be expressed as a linear combination of orthonormal basis vectors as follows:
where:
∣v(i)⟩are the orthonormal basis vectorsand
c(i)are complex coefficients
On measuring this quantum system, its state will collapse into one of its orthonormal basis vectors with a probability of ∣c(i)∣².
Checking For Orthonormal Basis Vectors
To check if two ket vectors ∣v1⟩ and ∣v2⟩ form an orthonormal basis:
Verify Orthogonality
To check if these ket vectors are orthogonal, their inner product must be 0.
2. Verify Normalization
To check if each ket vector is of unit length or normalized, its inner product with its corresponding bra must be 1.
3. Checking Span
n orthonormal vectors are needed as basis vectors for an n-dimensional Hilbert space.
This means two orthonormal vectors are needed as the basis for a 2-dimensional space.
And that just two orthonormal vectors cannot be the basis that form a 3-dimensional space.
4. Checking Linear Independence
Both vectors should be linearly independent.
This means that neither can be written as a scalar multiple of the other.
Or, no scalar c should satisfy the equation:
An Example: Checking For Orthonormal Basis Vectors
Consider two ket vectors:
Checking Orthogonality
This shows that they are orthogonal.
2. Checking Normalization
This shows that they are normalized.
3. Checking Span
The vectors ∣v1⟩ and ∣v2⟩ span a 2-dimensional space.
4. Checking Linear Independence
They are linearly independent because no scalar c satisfies:
We can see that these vectors form the standard orthonormal basis for a 2D Hilbert space.
These are conventionally called |0> and |1>, respectively and represent the computational basis states for a single qubit.
Show Me More Basis Vectors
Some other sets of basis vectors (called bases as plural) that we will use in quantum computing are denoted by the following terms:
Ordered vs. Unordered Basis
An Ordered basis is a set of basis vectors where their order is explicitly specified.
It is denoted by round brackets.
An Unordered basis, on the other hand, is a set of basis vectors that can be listed in any order without distinction.
It is denoted by curly brackets.
Note that:
But,
Ordered basis is important because changing the order of basis vectors changes the interpretation of the measurement of quantum systems.
Length Of Vector In Terms Of An Orthonormal Basis
We know that any ket vector can be expressed as the linear combination of the basis vectors, as shown below:
The length of this ket vector can be simply represented as:
On value substitution, we get the following formula for the length (norm) of the vector:
Finding Coefficients Of Linear Combinations of Basis Vectors
Starting again from the following linear combination of basis vectors:
The terms c(1) to c(n) are the Coefficients of basis vectors.
These coefficients are also called Probability amplitudes.
The square of these Probability amplitudes tells the likelihood of the vector ∣v⟩ “collapsing” into the corresponding basis state ∣b(n)⟩ during a measurement.
There’s a simple formula to find the value of these coefficients using the inner product of the corresponding basis vector with the original vector:
And the equation for the linear combination of basis vectors can be rewritten as:
There’s an easy way to calculate this.
The basis vectors can be represented as the columns of a matrix A as follows:
Then, the coefficients of |v> onto the basis can be calculated using the inner product of the transpose of matrix A with |v>.
The overall equation, therefore, becomes:
That’s everything for this short lesson on Orthonormal basis vectors used extensively in Quantum computing.
See you in the next one. Stay tuned!