Here’s the fourth part of the series that introduces all the mathematics you must understand to start doing quantum mechanics and quantum computing.
Here are the previous ones, in case you missed them:
Lesson 4: Probability
Probability measures the likelihood of an event happening.
For an event A to occur, its probability is given by:
if all events are mutually exclusive and all outcomes are equally likely.
If P(A) = 0, the event will never occur (impossible event)
If P(A) = 1, the event will undoubtedly occur (certain event)
For a coin toss given by a set {H,T}, where H is Head and T is the Tail of the coin, the probability of the event of getting Head is 0.5 or 50%.
The Complement Rule
The probability of an event not occurring (A’) is given by:
where P(A) is the probability of the event occurring.
For example, the probability of getting head in a fair coin toss is 0.5.
This makes the probability of getting a tail: 1 — 0.5 = 0.5
The Addition Rule
This rule is used to find the probability of the union of two events.
For two events, A and B, the probability of their union A ∪ B ( all outcomes that are in the set A, B, or both) is given by:
where:
P(A) is the probability of event A
P(B) is the probability of event B
P(A ∩ B) is the probability of both A and B occurring (Intersection).
For those new to the concepts of Union and Intersection in Set Theory, these are represented by the following diagrams:
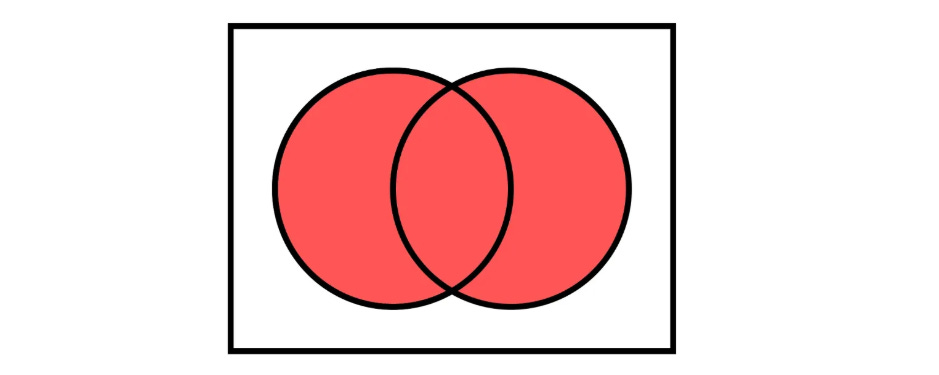
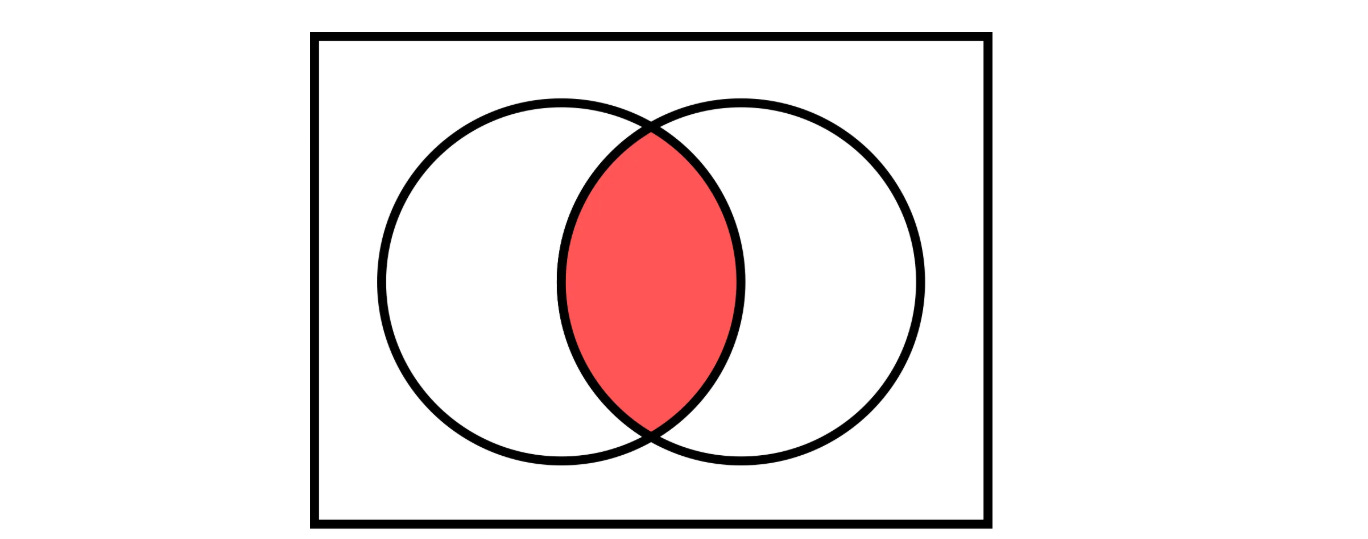
Let’s take an example where we draw a card from a deck of 52 cards.
The probability that of the event A when the card is a heart card is P(A) = 13 / 52 = 0.25
The probability that of the event B when the card is a face card is P(B) = 12 / 52 = 0.23
Then, for A ∩ B or the event when the card is a face card, and a heart card is:
P(A ∩ B) = 3/52 = 0.058
Using the addition rule, the probability of the card being either a heart or a face card is given as follows:
The Addition Rule For Mutually Exclusive Events
If the events A and B are mutually exclusive (or they cannot happen at the same time), in this case, the addition rule simplifies to:
This is because P(A ∩ B), i.e. the probability of both A and B occurring together, goes to 0.
Let’s say that we roll a dice.
The probability of the event A where we roll a 1 is given by P(A) = 1 / 6
The probability of the event B where we roll a 6 is given by P(B) = 1 / 6
Since both events are mutually exclusive, i.e. we cannot roll both a 1 and a 6 together, the probability of the result being either 1 or 6 is given as follows:
The Multiplication Rule
This rule is used to calculate the probability of two events occurring together or their Intersection.
For any two events A and B, the probability of both events occurring is:
where:
P(A) is the probability of event A
P(B ∣ A) is the probability that event B will occur, given that A has already occurred (conditional probability)
Let’s take an example.
If we draw two cards from a deck of 52 cards:
The probability of event A, when the card is an ace, is P(A) = 4 / 52 = 1 / 13
The probability of event B, when the card is an ace if the first card was also an ace, is as follows.
Here P (B | A) = 3 / 51 because only three aces remain in the second draw, as we already took out an ace in the first draw.
The Multiplication Rule For Independent Events
If A and B are independent events (the occurrence of one does not affect the probability of the other), then the Multiplication rule simplifies to:
For example:
When we roll a die, the probability of an event A of getting 6 is P (A) = 1 / 6.
When we flip a coin, the probability of an event B of getting heads is P (B) = 1 / 2.
The probability of both these independent events occurring is:
#/media/File:Venn0111.svg){kind=link}
We will learn the use of Probability in Quantum computing in the comming lessons.
See you soon in the next one!
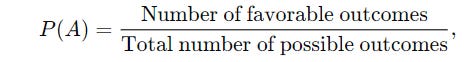
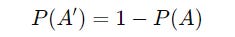
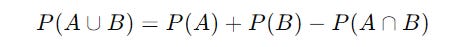
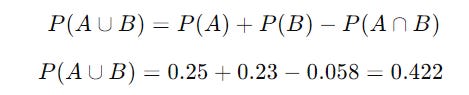
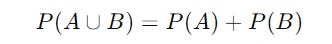
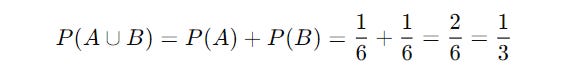
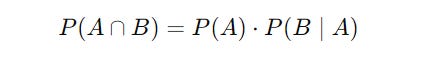
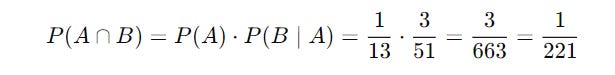
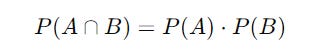
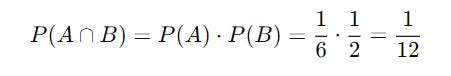
Nice post. A suggestion: it would've been nice to derive these rules from a set of axioms, and discuss the interpretation of the axioms and of probability itself, since this is not trivial.
Kudos