All The Math That You Need To Start Doing Quantum Computing (Part 6)
Lesson 6: Linear Algebra (2)

In this lesson, we further discuss concepts from Linear Algebra that are essential for learning about Quantum systems.
In case you missed the previous lessons on the mathematics required for quantum mechanics and quantum computing, here they are:
Lesson 6: Linear Algebra (2)
Determining Orthogonality
The term ‘Orthogonal’ means Perpendicular.
Using the Pythagorean theorem, two ket vectors |v> and |w> are orthogonal or perpendicular to each other, if and only if:
There’s another way of determining the Orthogonality of two vectors, which we will discuss soon in the next section.
Scalar Multiplication
For a ket |v>, multiplying it with a scalar term/ number c gives:
This operation is the same as the bra <v| being multiplied by c*, the complex conjugate of c.
Let’s take an example.
For
Scalar multiplication of |v> is given by:
Scalar multiplication of the bra ⟨v∣ = (1 −i) is given by:
You must be wondering what the utility of this operation is.
Scalar multiplication is used to obtain vectors of different lengths pointing in the same direction as the original vector.
For example, for a bra <v|, multiplying it with 0.5 and 3 will give us half and three times longer vectors pointing in the same direction as <v|, respectively.
Finding A Unit Vector Pointing In A Given Direction
An important utility of scalar multiplication is to find a unit vector (vector on length 1) pointing in the direction of a non-unit vector.
For a non-unit ket |v> , a unit vector |u> that points in the same direction is given by:
where:
∣u⟩is the unit vector (called Normalized ket)∥v∥is the length (norm) of the vector
The length (Euclidean norm) can be calculated as follows, but for ket vectors, there’s another formula that we will learn in the next section.
If you’re new to linear algebra, unit vector, normalized vector, and vector of length 1, they all mean the same.
Vector Multiplication Using The Inner Product
The multiplication of a bra ⟨v∣ and a ket ∣w⟩ is called the Inner or Dot product.
The result is a scalar value (usually a complex number).
where:
v*(1)tov*(n)are the complex conjugates of thei-th element of the bra<v|
(Remember that these are obtained from complex conjugation of the elements of |v>.)
w(1)tow(n)are the elements of the ket|w>
Vector Multiplication Using The Outer Product
The multiplication of a ket ∣v⟩ and a bra ⟨w∣ is called the Outer Product.
The result is a matrix or an Operator.
It can also be represented as:
|v> ⊗ <w|
The outer product is a specific case of the tensor product.
The tensor product is a more general operation that works with tensors of any rank.
Rank-1 tensor: A vector (1D array)
Rank-2 tensor: A matrix (2D array)
Rank-3 tensor: A 3D array
Rank-N tensor: A multi-dimensional array requiring N indices to access its elements.
Determining Length Using The Inner Product
The length of a ket |v> can be determined using the square root of its inner product with its corresponding bra.
This is the same as the length-finding operation that we learned earlier.
where:
v(1)tov(n)are the elements of|v>v*(1)tov*(n)are the complex conjugate elements of<v|
For example, for a ket, as shown below:
Its length is calculated as follows:
An important use of this formula is determining if a ket is of unit length.
A ket is a unit vector if and only if the square root of its inner product with itself equals 1.
Determining Orthogonality Using The Inner Product
Two vectors are orthogonal if and only if their inner product is 0.
This can be derived from the formula that we discussed previously:
The lesson on Linear algebra is broken down into different parts to make it easy to learn.
Stay tuned for the next part!


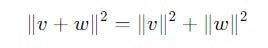
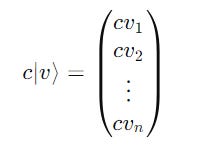
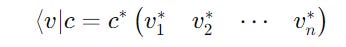
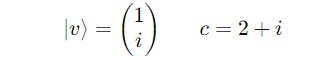
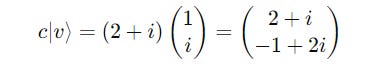
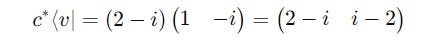
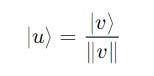
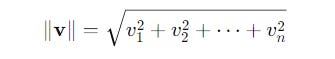
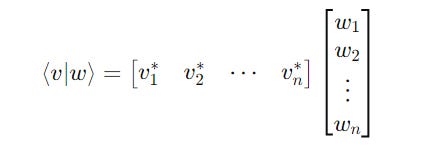
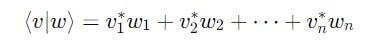
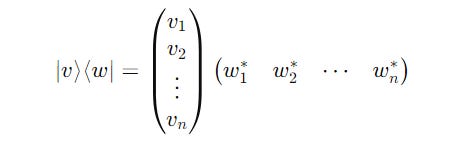
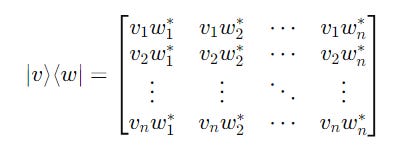
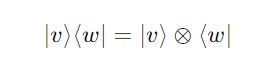
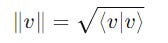
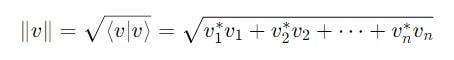
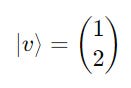
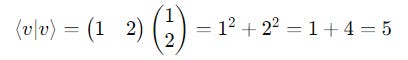
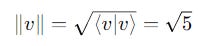
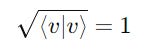
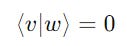

Well-done, is there anyway quantum computing and manufacturing (addictive manufacturing) can work together? Thanks