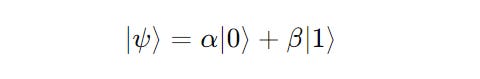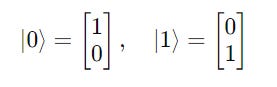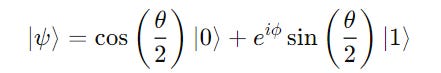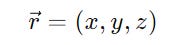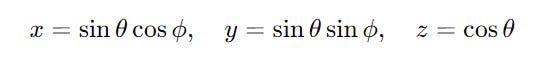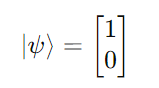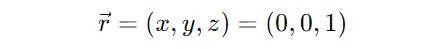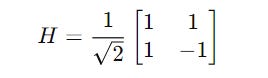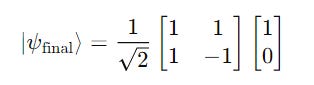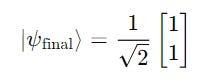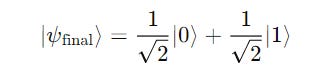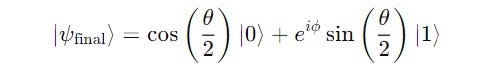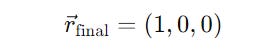If you’ve been a student of classical Physics, you must have plotted the state of a particle in a 3D Cartesian space.
But unlike a classical particle here, a quantum system is represented using a Hilbert Space.
A Hilbert Space is a vector space with either a finite or infinite number of dimensions.
Its elements are Kets, which represent quantum systems.
(If you’re unfamiliar with Ket and Bra vectors, starting with the lesson titled “An Introduction To Bra-Ket (Dirac) Notation” is highly recommended.)
Visualizing The Hilbert Space
A single qubit can be represented using a 2-dimensional Hilbert space.
Just like i and j, which are basis vectors for a classical 2D space, the basis vectors for a 2D Hibert space representing a qubit are ∣0⟩ and ∣1⟩.
Similar to i and j, these are orthonormal to each other.
Ortho: Perpendicular to each other
Normal: Their length is 1, or they are Unit vectors.
Any vector (ket) in the Hilbert space can be written as a linear combination of the basis vectors.
A ket for a single qubit can be represented as:
where:
∣0⟩ and ∣1⟩ are basis vectors
By convention, these can be represented by the following kets.
α and β are Probability amplitudes (complex numbers)
To visualise this 2-D complex Hilbert space on a 3-D real (not complex) space and make it more intuitive, we use something called the Bloch Sphere.
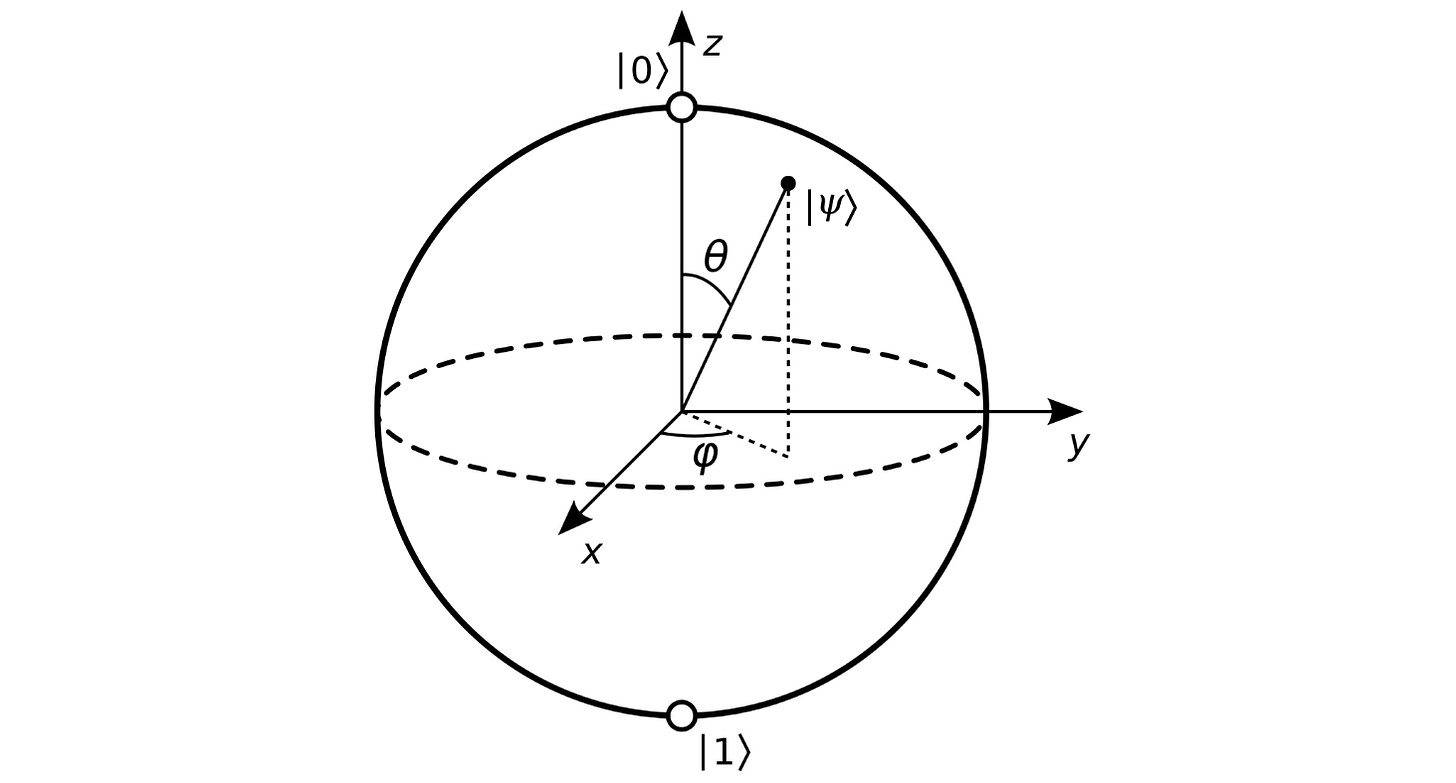
The representation of our qubit on the Bloch sphere is given by:
where:
θ is the angle between the qubit state and the ∣0⟩ axis
ϕ is the rotation of the state around the z-axis
e^(iϕ) is the relative phase between ∣0⟩ and ∣1⟩
To map ∣ψ⟩ from Hilbert space to a point on the Bloch sphere, we use a real-valued unit vector denoted using r.
where:
Consider some examples of representations on a Bloch sphere.
∣ψ⟩ = ∣0⟩ will be represented by r = (0, 0, 1) (point on the North pole)
∣ψ⟩ = ∣1⟩ will be represented by r = (0, 0, -1) (point on the South pole)
∣ψ⟩ in a superposition as (1/√2)(∣0⟩ + ∣1⟩), will be represented by r = (1, 0, 0) (Point on the equator along the x-axis)
∣ψ⟩ in a superposition as (1/√2)(∣0⟩ - ∣1⟩), will be represented by r = (-1, 0, 0) (Point on the equator along the negative x-axis)
Why Use The Bloch Sphere?
The visual representation of a qubit using the Bloch sphere is really important because all the operations we will perform in the Hilbert space can correspond to rotations of the vector r on the Bloch sphere.
Let’s learn this with an example.
For a qubit in the state ∣ψ⟩ = ∣0⟩ in the Hilbert space (also represented using the ket as follows):
On the Bloch sphere, it is represented as:
This lies on the North Pole of the sphere.
When we apply the Hadamard gate (you do not need to know what it is for now) represented by the following matrix:
The following matrix multiplication occurs:
The result is a state of equal superposition, shown below.
Using the Bloch sphere representation equation as discussed previously:
We can calculate:
This lies on the equator, along the x-axis.
This means that the Hadamard gate rotated the Bloch vector from the north pole to the equator along the positive x-axis.
This is the same as it starting from ∣0⟩ and creating an equal superposition state (1/√2)(∣0⟩ + ∣1⟩).
Further Reading
If you’re more mathematically inclined and would love a detailed lesson on Hilbert spaces, the following would help:
See you soon in the next lesson!
