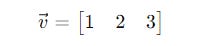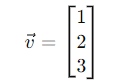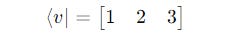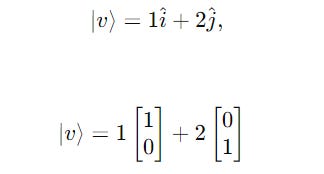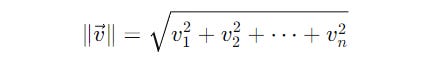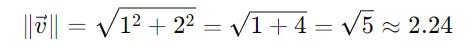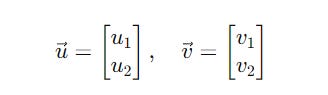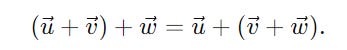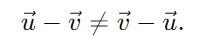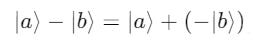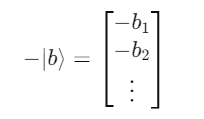All The Math That You Need To Start Doing Quantum Computing (Part 5)
Lesson 5: Linear Algebra (1)
In case you missed the previous lessons on the mathematics required for quantum mechanics and quantum computing, here they are:
Lesson 5: Linear Algebra (1)
What Are Vectors?
Vector is an ordered list of n numbers.
These numbers that make up a vector are called Entries or Elements of that vector.
The number n is called the dimension of the vector.
The term representing a vector has an arrow on its top.
Based on their arrangement, vectors can be classified as:
Row vectors (called Bras)
Column vectors (called Kets)
(If you’re unfamiliar with Bra-Ket notation, I recommend reading this lesson first.)
In the Ket notation, a vector is written as |v>:
In the Bra notation (conjugate transpose of the ket), this vector is written as <v|:
Since we are discussing Quantum mechanics, I will often talk about Bra and Ket notation from here on.
Vectors In Euclidean Space
Basis vectors of a Euclidean space are:
Linearly independent
Orthogonal to each other
of Unit length (their length is 1)
For a 2D space, the basis vectors are i and j along the x-axis and y-axis, respectively, and so on.
Any vector can be written as a linear combination of the basis vectors in an Euclidean space.
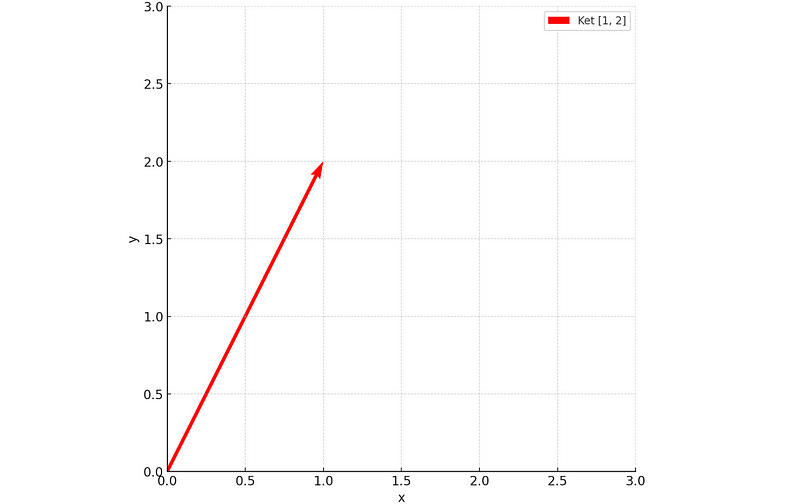
For a ket |v>, as shown below:
It can be expressed using basis vectors as follows:
The vector can be plotted as follows:
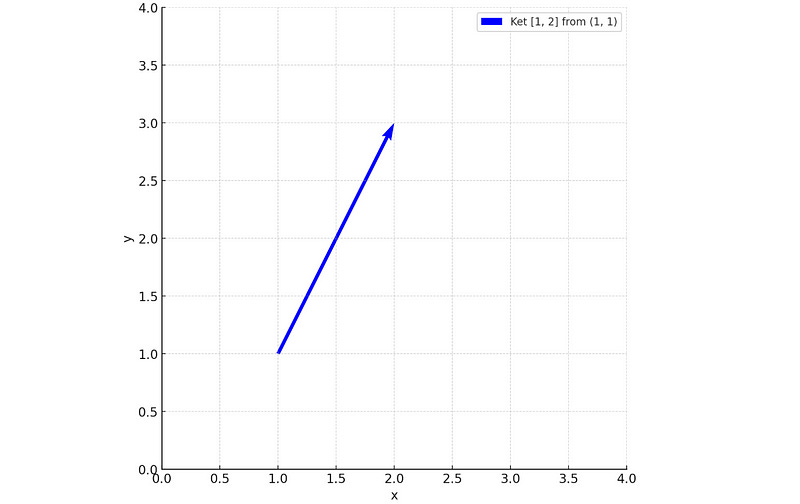
The vector doesn’t necessarily have to be plotted on the origin; its starting point can be anywhere else on the plane.
Length Of A Vector
The length of a vector (called Magnitude or Norm) of a vector v is represented by ||v||.
It is calculated as follows:
The formula for length calculation is derived from the Pythagorean theorem.
For a vector with elements [1, 2], its length can be calculated as follows:

A unit vector has a length of 1. For example, ||i|| = 1 .
The length of a ket vector is calculated using its inner product with its corresponding bra. (We will return to this statement in the next lesson when discussing vector multiplication.)
Vector Addition and Subtraction
For two ket vectors u and v as shown below:
Their elements can simply be added as follows:
A similar operation can be performed to subtract them:
Similarly, for two bra vectors shown below:
These can be added as follows:
Similarly, then can be subtracted as follows:
It is important to note that vector addition is commutative, which means that the order of addition doesn’t matter:
It is also associative, which means that the grouping of vectors doesn’t matter:
But subtraction is neither commutative nor associative.
The Parallelogram Law
This is a geometric rule that states that:
The sum of two vectors can be represented by the diagonal of a parallelogram formed these vectors as adjacent sides.
|a> + |b> can be performed using the law and creating a parallelogram as follows:
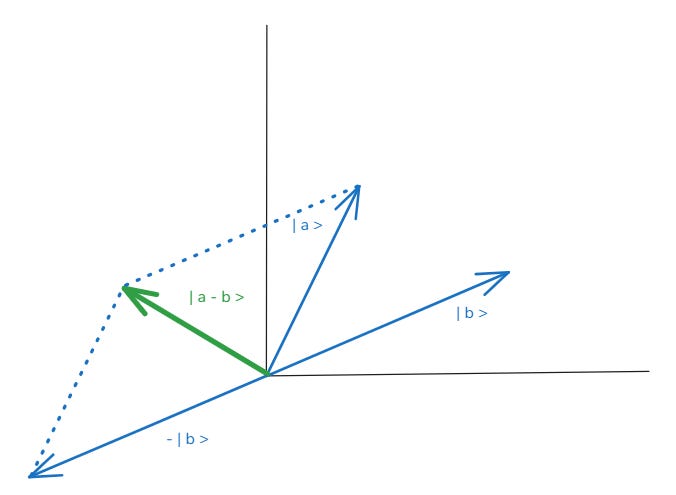
The same rule can be extended to subtraction as follows:
where
Triangle Law Of Vector Addition
This law is a special case of the parallelogram law of vector addition.
It is used to find the sum of two vectors by representing them as two sides of a triangle.
The third side obtained in the sum of the other two vectors.
The lesson on Linear algebra is broken down into different parts to make it easy to learn.
Stay tuned for the next part!