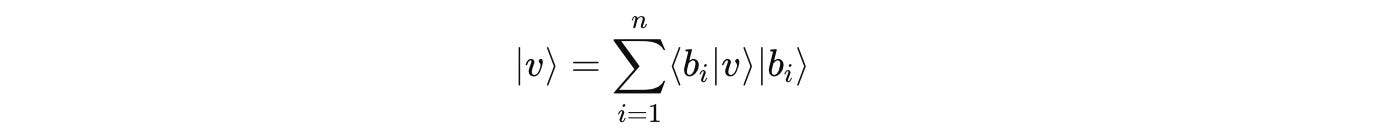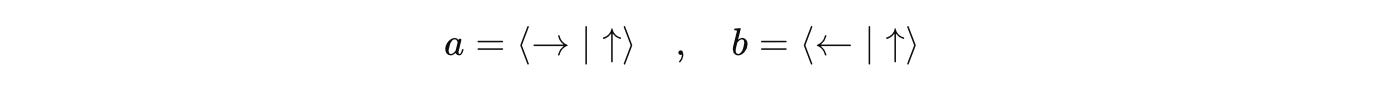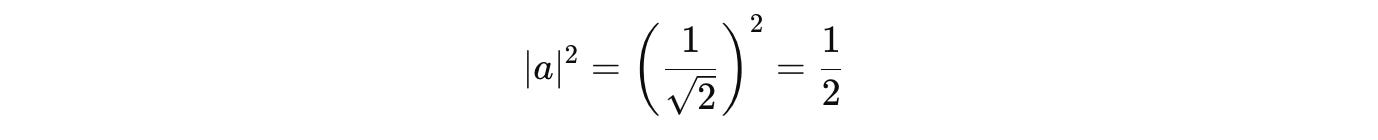A Mathematical Lesson On How Measurements Affect A Qubit
Use Linear Algebra on a Qubit to learn how it transforms upon being measured
We have learned all the mathematics needed to understand quantum systems in a series of 10 lessons.
In this lesson, it’s time to track a qubit, learn to measure its state on different orthonormal bases, and mathematically learn how measurements affect it.
In case you missed the previous lessons, here they are:
An Electron As A Qubit
An electron has an intrinsic property called the Spin that can represent a Qubit in quantum computing.
Note that this does not literally mean that the electron is physically spinning in space. Instead, it just represents a fundamental aspect of its quantum state.
When measured along a specific axis (typically the Z-axis), the spin of an electron can be found in one of two states:
Spin-Up (
∣↑⟩): Aligned with the positive direction of the measurement axis (e.g., pointing up along the Z-axis on the standard orthonormal basis).Spin-Down (
∣↓⟩): Aligned against the positive direction, pointing down along the negative Z-axis on the standard orthonormal basis.
These two states form the computational basis for a single qubit system.
|0⟩ or ∣↑⟩ and |1⟩ or ∣↓⟩ are the quantum analogues of the classical binary states 0 and 1.
(In the complex vector space C², the standard orthonormal basis and the computational basis are the same.)
But there’s a little nuance here.
A qubit can exist in a superposition of these states.
This is represented using the ket ∣ψ⟩.
When measured, the qubit collapses to either |0⟩ or |1⟩ with probabilities ∣α∣² and ∣β∣², respectively.
Btw, my book “Computer Science In 100 Images” is currently available at a 40% discount for early readers. Grab your copy using this link.
The Experiment
Let’s run an experiment on an electron initially in the Spin-up state.
Step 1: Measuring In Vertical Axis
When we measure it using an apparatus (which can be a magnetic field gradient) aligned along the vertical direction, ∣α∣² will be 1, or the measurement result will always be Spin-up with probability 1.
Also ∣β∣² will be 0, or the probability that the qubit is in the Spin-down state will be 0.
Step 2: Measuring In Horizontal Axis
Next, we turn our measuring apparatus, aligning it along the horizontal/ X-axis.
The orthonormal basis for measuring spin in the horizontal direction is represented using ∣→⟩ and |←⟩, as shown below.
Or,
On measuring along this direction, the Spin-up qubit gets in a superposition state of the horizontal basis as follows:
Our task now is to find how much of this Spin-up electron is in the positive horizontal state and how much is in the negative.
This can be done by finding the coefficients a and b.
To express a given ket, let’s say, ∣v⟩ as a linear combination of an orthonormal basis { ∣b(1)⟩, ∣b(2)⟩, … , ∣b(n)⟩ }, the following formula can be used:
In the above equation, ⟨b(i)∣v⟩ represents the inner product (or projection) of ∣v⟩ onto the basis vector ∣b(i)⟩.
Using this, let’s reformulate the representation of the Spin-up electron on the horizontal axis.
Now, our task is to calculate a and b, where:
We calculate ‘a’ as follows:
We calculate ‘b’ as follows:
This leads to the following superposition state for the Spin-up electron when measured along the horizontal axis:
In this state, the square of the coefficients a and b gives the probabilities of finding the electron in the positive and negative horizontal/ X-axis, respectively.
In either case, the probability of ending up with either of the horizontal states is 50%.
Step 3: Measuring Again In The Vertical Axis
Let’s again measure using the vertical basis {∣↑⟩, ∣↓⟩}.
In the last step, we obtained ∣→⟩ and |←⟩, with equal probabilities.
Keep reading with a 7-day free trial
Subscribe to Into Quantum to keep reading this post and get 7 days of free access to the full post archives.