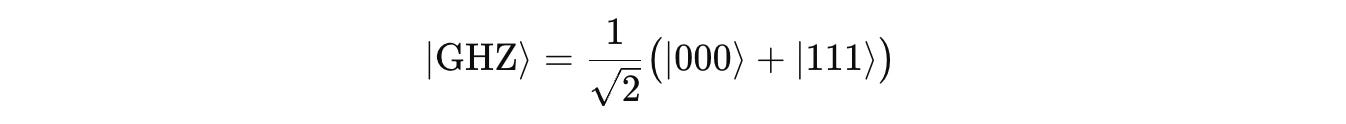Build The Greenberger–Horne–Zeilinger (GHZ) State Using Qiskit
Solution to Question 5 of the ongoing Quantum programming challenge.
Hey there!
I recently published a challenge with 6 Qiskit questions to get started with Quantum Computing.
Here is the solution to the 5th question from the challenge.
Question 5
Create a three-qubit Greenberger-Horne-Zeilinger (GHZ) state in Qiskit.
Measure and simulate the circuit using a Qiskit simulator.
What is the Greenberger–Horne–Zeilinger (GHZ) State?
A GHZ state (Greenberger–Horne–Zeilinger state), named after the three authors who first described this state, is a multi-qubit entangled quantum state that involves three or more qubits.
For the 3-qubit case, it is mathematically described as:
For n > 3 qubits, it is mathematically described using the general form:
GHZ states are used to demonstrate quantum non-locality among multiple parties and in secure quantum communication protocols such as multi-party quantum secret sharing (QSS).
Solution
Let’s create a three-qubit Greenberger-Horne-Zeilinger (GHZ) state in Qiskit.
We start by creating a circuit with 3 qubits and 3 classical bits to store measurement results.
from qiskit import QuantumCircuit
circuit = QuantumCircuit(3, 3)At this point, all qubits (q(0), q(1) and q(2)) are in state |0>.
Next, we put qubit 0 or q(0) into an equal superposition state using the Hadamard gate.
circuit.h(0)Qubit 0 now looks as follows:
Next, we consider the joint state of q(0) and q(1) and apply the CNOT gate to it, with q(0) as the control and q(1) as the target.
The CNOT (Controlled-NOT) gate flips the target qubit if and only if the control qubit is in state |1>.
Applying CNOT results in:
This is the Bell state |Φ+>.
We perform these operations in Qiskit as follows:
circuit.cx(0, 1)Then, we consider the 3rd qubit along with the previously created Bell state and apply the CNOT gate using q(0) as the control and q(2) as the target.
Apply CNOT results in:
We perform these operations in Qiskit as follows:
circuit.cx(0, 2)This results in the GHZ state.
Finally, we measure all qubits and store their results in the corresponding classical bits
circuit.measure([0, 1, 2], [0, 1, 2])This is how the circuit and all its operations look.
print(circuit.draw()) ┌───┐ ┌─┐
q_0: ┤ H ├──■────■─────┤M├───
└───┘┌─┴─┐ │ ┌─┐└╥┘
q_1: ─────┤ X ├──┼──┤M├─╫────
└───┘┌─┴─┐└╥┘ ║ ┌─┐
q_2: ──────────┤ X ├─╫──╫─┤M├
└───┘ ║ ║ └╥┘
c: 3/════════════════╩══╩══╩═
1 0 2 The numbers at the bottom show which classical bit each qubit’s measurement is stored in. Note that this sequence does not represent the time order of measurements. It simply shows how each qubit’s measurement is mapped to a classical bit.
Now that we have created the quantum circuit, it is time to simulate it on the quantum simulator.
from qiskit_aer import AerSimulator
from qiskit import transpile
# Instantiate Qiskit quantum simulator
simulator = AerSimulator()
# Transpilation
transpiled_circuit = transpile(circuit, simulator)
# Execute the circuit on the simulator for 1024 repetitions
result = simulator.run(transpiled_circuit, shots=1024).result()
# Get the measurement results
counts = result.get_counts()
print("Counts:", counts)
# Counts: {'111': 507, '000': 517}We run the simulations for 1024 independent shots. The counts value represents how many times each outcome occurred during these shots.
These outcomes are visualised as follows.
from qiskit.visualization import plot_histogram
plot_histogram(counts)We calculate the probabilities for each outcome as follows.
# Calculate probabilities
total_shots = sum(counts.values())
for outcome, count in counts.items():
probability = (count / total_shots) * 100
print(f"|{outcome}⟩: {count} counts ({probability:.1f}%)")
"""
Output:
|111⟩: 507 counts (49.5%)
|000⟩: 517 counts (50.5%)
"""When we measure all three qubits, we observe 000 and 111 with each occurring about 50% of the time as expected.
That’s everything for this article.
Thanks for being a curious reader of ‘Into Quantum’, a publication that teaches essential concepts in Quantum Computing from the ground up.
To get even more value from this publication, consider becoming a paid subscriber.