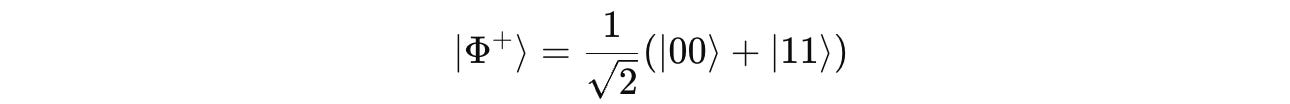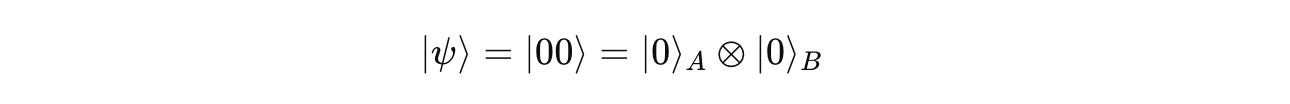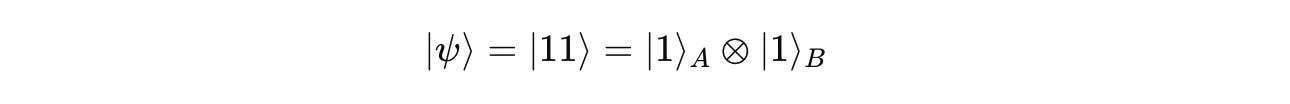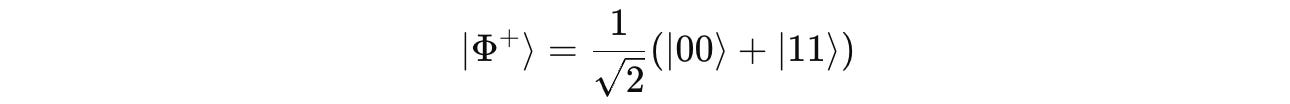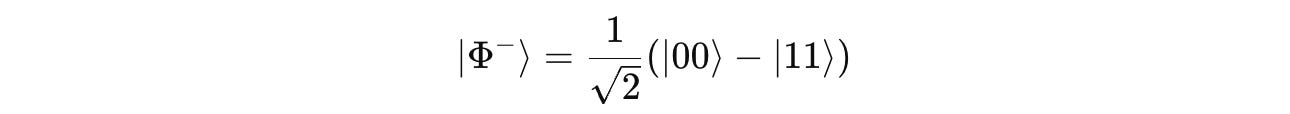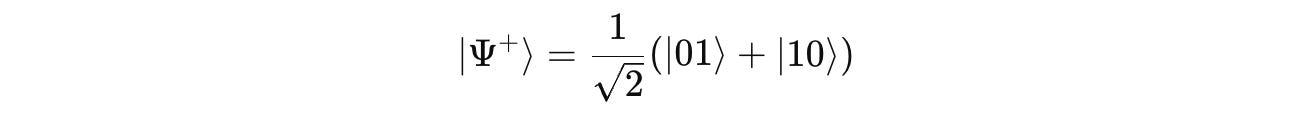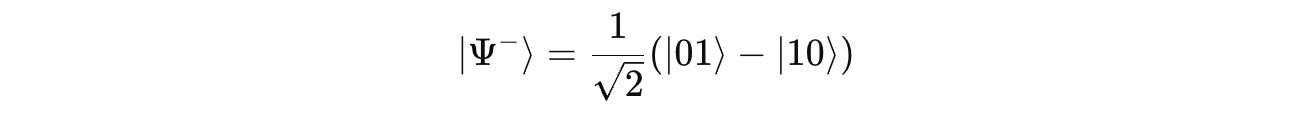What Are Bell States & How To Express Quantum Systems Using Them
Let's explore Bell states popularly used in Quantum Teleportation and Superdense Coding.

Bell states are maximally entangled two-qubit states, named after the physicist John Stewart Bell.
‘Entanglement’ means that the measurement of just one qubit instantaneously affects the other, regardless of how far apart they are placed.
‘Maximally entangled’ means that the two qubits are fully correlated, or knowing everything about one tells us everything about the other.
Take an example of a Bell state |Φ+> as follows:
It is a maximally entangled state of two qubits (let’s call them A and B).
When we measure |Φ+>, the system either collapses into |00> or |11> with a 50% (1/2) chance for each since their probability amplitude is 1/√2.
If we get the state |00>, this is a combination as shown below:
This means that both qubits A and B will be |0>.
Similarly, if we get the state |11>, this is a combination as shown below:
This means that both qubits A and B will be |1>.
Both of the qubits are perfectly correlated, or maximally entangled.
My latest book, called “LLMs In 100 Images”, is now out!
It is a collection of 100 easy-to-follow visuals that describe the most important concepts you need to master LLMs today.
Grab your copy today at a special early bird discount using this link.
The Four Bell States
There are four Bell states, and their Dirac notations are shown below:
Φ⁺(Phi plus)
2. Φ⁻ (Phi minus)
3. Ψ⁺ (Psi plus)
4. Ψ⁻ (Psi minus)
Bell states are used in:
Quantum Key Distribution (QKD) protocols, such as the BBM92 protocol used in Cryptography
Superdense Coding that allows someone to send two classical bits of information to another by transmitting only one qubit
Quantum Teleportation that transfers a particle’s quantum state to another location without moving the particle itself