God Does Play Dice With The Universe
Principle 2: Measurements of Quantum systems are truly random
I have a question for you (and many would think it’s silly).
Are the results of tossing a coin random?
Although we have been taught that that is it from a very young age, the answer is No.
Then why is it considered random for practical purposes? — you’d ask.
To answer this, let’s understand how a coin toss works.
The Classical Physics Behind A Coin Toss
The trajectory of a tossed coin can simply be described using Newton’s equations of motion:
where:
Fis the force acting on the coin from the tosser’s thumbmis the mass of the coinais the acceleration of the coin due to this force
But there’s more to it.
The motion of the coin also depends on the —
Torque applied by the tosser’s thumb
Air resistance
The elasticity of the coin and more
Theoretically, all of these variables can be measured, and the exact result of the coin toss can be obtained in an experiment.
Thus, the result of a coin toss is deterministic or non-random.
The issue is the large number of initial variables and the high sensitivity of the final result to changes in these variables, which makes it tough to do so.
Small uncertainties in the initial conditions of the coin toss lead to big differences in the result. (This is called Chaos Theory.)
This makes a coin toss random for practical purposes, even when it is not truly random.
What Is True Randomness Then?
Let’s talk about quantum entities.
We know from the previous lesson that a quantum system can exist in a superposition of multiple states.
The wave function of the quantum system can be described as:
where:
c(1)andc(2) are complex coefficientsc(1)(ψ1)andc(2)(ψ2)the two eigenstates of the system
When this system is observed or measured, it is forced into one of its eigenstates.
The probability that the system will enter one of these eigenstates is given by the square of its preceding coefficient.
Although these states' outcomes are based on these probabilities, what happens to the system when it is measured each time is truly random.
For example, if we measure an electron's spin, we can tell how probable it would be for each electron’s wave function to collapse into one of the eigenstates. However, the result of an individual measurement will be truly random.
Einstein Hated Quantum Randomness
When Einstein encountered this phenomenon for quantum systems, we just could not accept it.
He famously said —
“God does not play dice with the universe.”
He believed that scientists were missing something.
Just like a coin toss, these were some hidden variables that were not obvious but, if known, could calculate a system’s measurement outcome precisely.
Unfortunately, Einstein was wrong.
In 1964, John Bell, a quantum physicist, proved that the hidden variables Einstein had in mind don’t exist.
The details of the experiment are for another lesson, but it gives compelling evidence that quantum systems show intrinsic randomness.
Next time, when you toss a coin, know it is not truly random. (You cheat!)
See you in the next lesson.



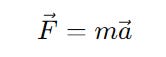
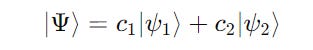
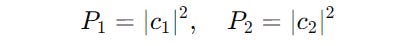

So can we infer that behind every random event, there is some bias which is not random?