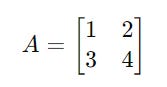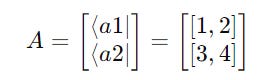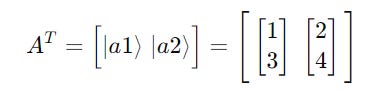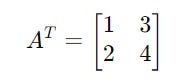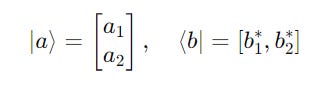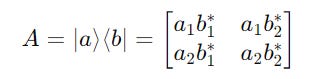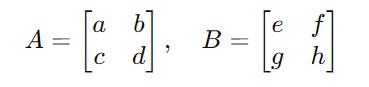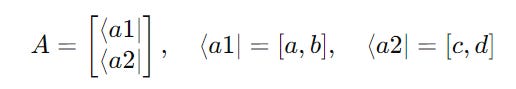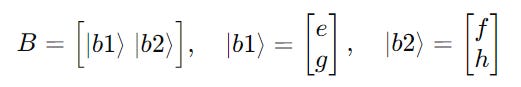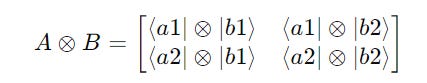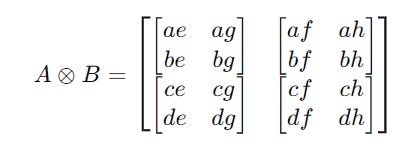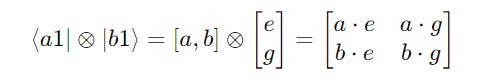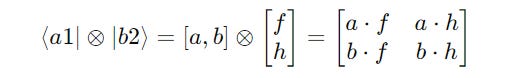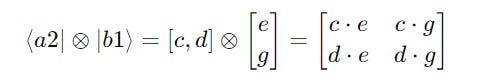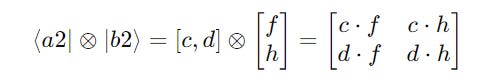All The Math That You Need To Start Doing Quantum Computing (Part 10)
Lesson 10: Linear Algebra (6) - More Operations On Matrices With Bra & Kets

In this lesson, we learn about matrices composed of bras and kets, and learn to perform further operations on them.
You should read this chapter with Lesson 7: Linear Algebra (3) to get the most out of it.
In case you missed the previous lessons on the mathematics required for quantum mechanics and quantum computing, here they are:
Lesson 10: Linear Algebra (6)
Matrix Transpose
This operation involves swapping the rows and columns of a matrix.
In bra-ket notation, this means transforming bras into kets and vice versa.
For matrix A:
It can be written as a stack of its bras as follows:
Transposing it turns these bras into kets as follows:
The final result is as follows:
Outer Product To Create Matrices
The outer product of a ket and a bra creates a matrix.
For a ket |a> and bra <b|:
Their outer product produces a matrix as follows:
Tensor Products Of Matrices
The tensor product (or Kronecker product) of two matrices combines them into a larger matrix.
For two matrices A and B:
Matrix A can be represented using bras as follows:
Matrix B can be represented using kets as follows:
Their tensor product is calculated as follows:
Further expanding them:
The calculations at the intermediate steps are shown below:
The lesson on Linear algebra is a short but important one.
Stay tuned for the next part!