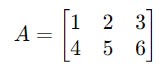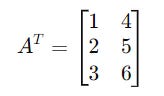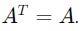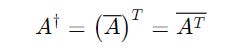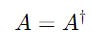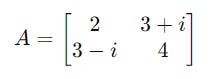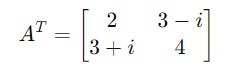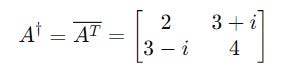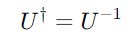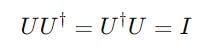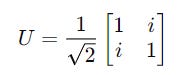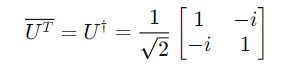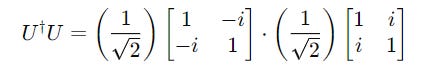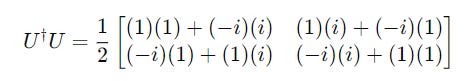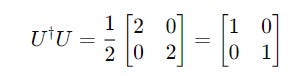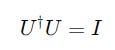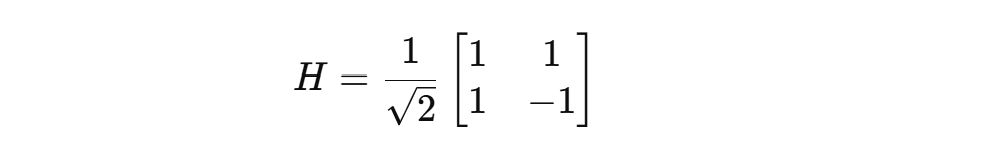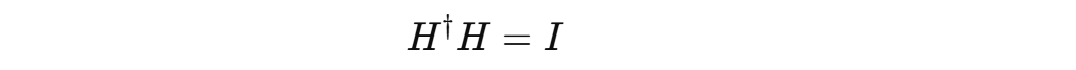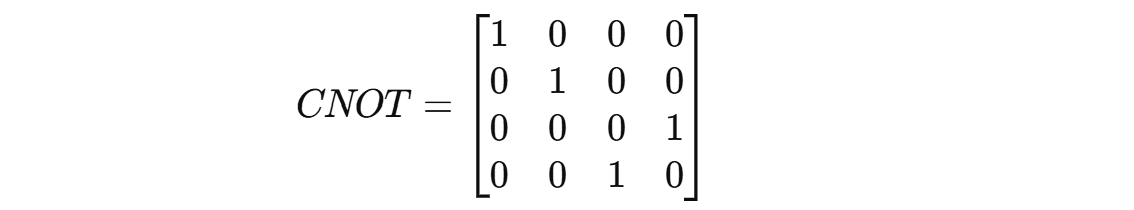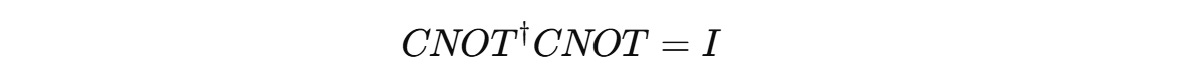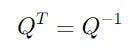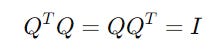All The Math That You Need To Start Doing Quantum Computing (Part 8)

Lesson 8: Linear Algebra (4) - Important operations on Matrices

Jan 19, 2025

undefined — Portrait of **Paul Dirac,** who formulated the **Dirac equation**, describing relativistic quantum mechanics and predicting the existence of antimatter. His work laid foundational principles for quantum mechanics, including **bra-ket notation**, which became essential in quantum computation and information theory. (Source)

In the last lesson, we introduced matrices and some common operations on them.

This lesson is about discovering more operations on Matrices specific to Quantum computing.

In case you missed the previous lessons on the mathematics required for quantum mechanics and quantum computing, here they are:

Lesson 8: Linear Algebra (4)

Matrix Transpose

Transpose of a matrix means creating a new matrix by flipping the rows and columns of the original matrix.

For a matrix A with dimensions 2 x 3 (2 rows and 3 columns):

Its transpose A^T has dimensions 3 x 2 (3 rows and 2 columns):

A matrix is called Symmetrical if it is equal to its transposed matrix.

Conjugate Transpose Of A Matrix

Conjugate transpose (also called Hermitian transpose/ Hermitian conjugate) combines:

Transpose or flipping the rows and columns of a matrix
Complex conjugation or replacing each element in a matrix with its complex conjugate

The dagger sign (†) represents this operation on a matrix.

where:

A(bar) is the complex conjugate of A
T is the transpose operation

A special type of matrix called the Hermitian matrix is related to this operation.

Hermitian Matrix

A Hermitian matrix is a square matrix that is equal to its conjugate transpose.

Consider a matrix A as follows:

Its transpose is calculated as:

Next, its complex conjugate completes the Conjugate transpose operation, leading to the following:

This is the same as A and hence A is a Hermitian Matrix.

Hermitian matrices represent observables (physical quantities that can be measured, such as spin, position, momentum, energy and more) in quantum mechanics.

This is because the eigenvalues of Hermitian matrices are all real numbers.

We will discuss this further in the upcoming lesson on Eigenvectors and Eigenvalues.

Unitary Matrix

A Unitary matrix is a square matrix whose conjugate transpose is its inverse.

It satisfies the following equation (we previously saw this when discussing the Identity matrix):

where:

U is a square matrix
U† is its inverse
I is the identity matrix

Consider the following matrix U:

Its conjugate transform is calculated as:

To check if the matrix U is Unitary, we do the following operation:

We arrive at the following conclusion:

Hence, the matrix U is a Unitary matrix.

In Quantum computing, Quantum gates are represented by Unitary matrices.

Two important quantum gates are:

Hadamard Gate
It is a 2 x 2 unitary matrix that operates on a single qubit (in a state of |0⟩ or |1⟩) and turns it into a superposition of both states.
where:
1. CNOT Gate
  It is a 4 x 4 unitary matrix that operates on two qubits where the first qubit (control qubit) determines whether to flip the second qubit (target qubit) or not.
  Again: