How to Rotate and Calculate Quantum Basis Vectors

Learn to calculate Quantum Basis Transformations using simple Trigonometric functions

Photograph of Werner Heisenberg, a pioneering physicist who formulated Matrix mechanics, developed the Uncertainty principle, and made significant contributions to quantum mechanics, earning him the 1932 Nobel Prize in Physics (Source)

In the previous story, we tracked how a qubit's state is changed when measured.

If you’re new to Quantum mechanics, here’s a little brief.

We represent a qubit’s state using the Computational basis (the standard orthonormal basis in the complex 2-D vector space) consisting of two orthonormal vectors:

Any qubit exists as a superposition of these vectors as follows:

In the above equation, α and β are complex numbers called Probability Amplitudes, the squares of whose magnitudes represent the probabilities of measuring the qubit in the respective states.

To avoid the “complexities” of the complex plane, let’s visualise this computational basis on the 2-D real plane.

---

What Happens When We Turn The Basis States To An Angle?

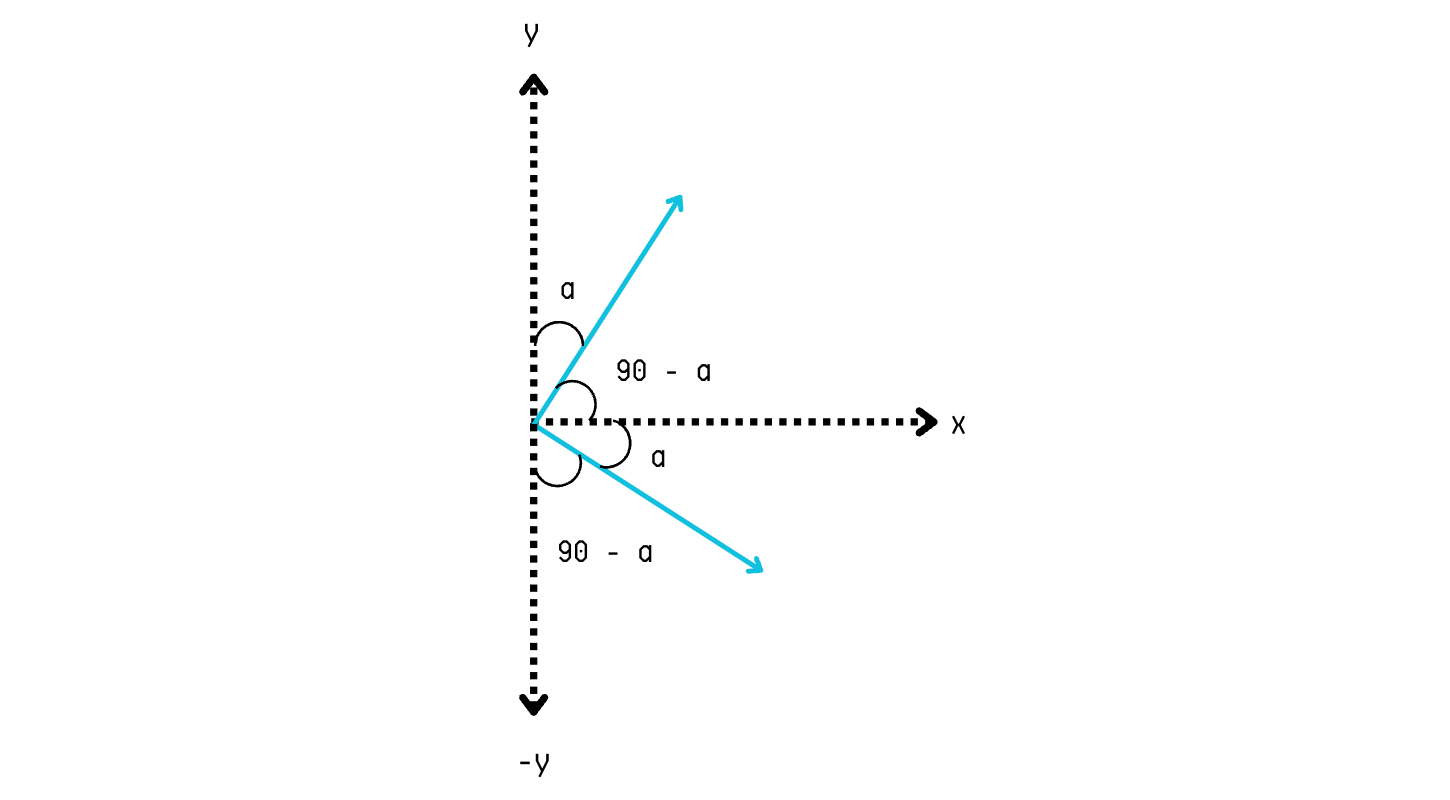
Let’s turn the basis vectors by an angle α.

The new basis vectors are shown in blue.

Using the lesson in Trigonometry, the basis vectors:

now become:

These are shown in the image below.

To rotate the basis by α, we will have to rotate the angle of the measuring device by an angle θ, where θ = 2α. This is due to how unitary transformations work on the Bloch sphere.

This results in the formula: