All The Math That You Need To Start Doing Quantum Computing (Part-2)
Lesson 2: Trigonometry
Here’s the second part of the series that introduces all the mathematics you must understand to start doing quantum mechanics and quantum computing.
Here’s the first one if you missed it.
Lesson 2: Trigonometry
Trigonometric functions define the relationships between angles and the ratio of lengths of a right-angled triangle.
Consider the right-angled triangle shown below:
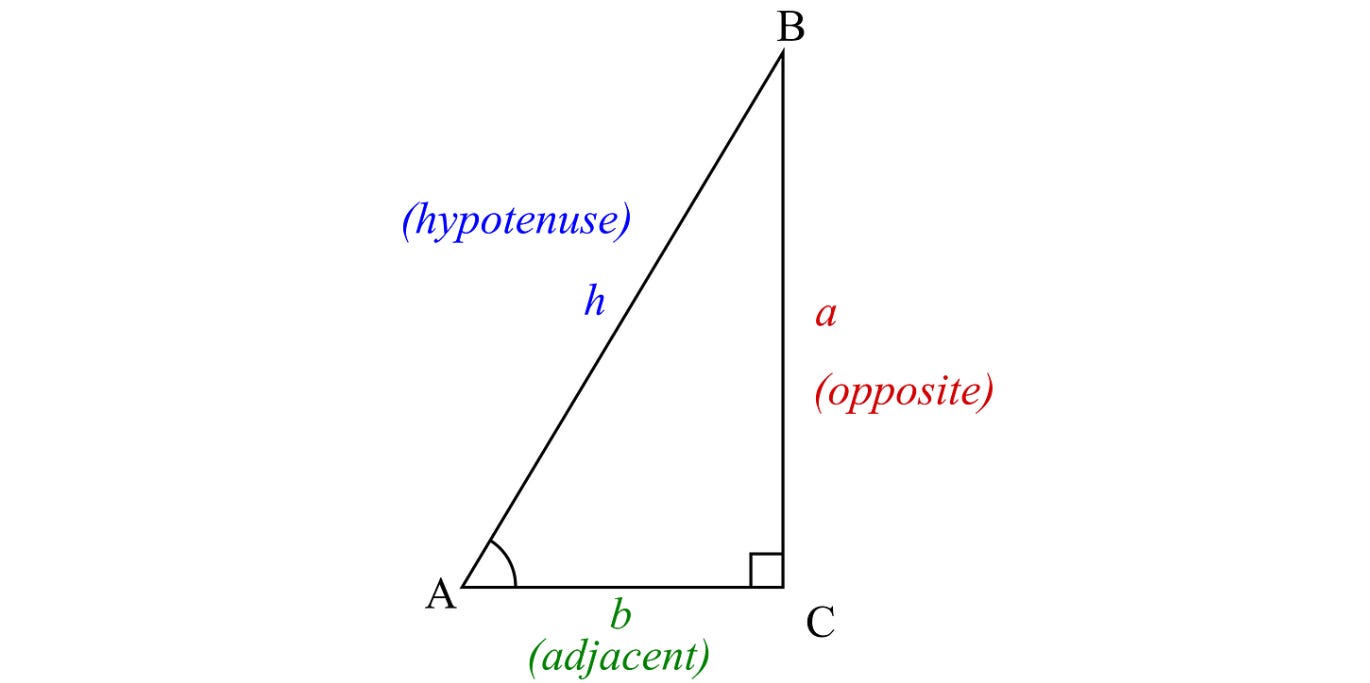
The trigonometric functions associated with this triangle are as follows:
The reciprocal to these functions are as follows:
where:
sinis sinecosis cosinetanis tangentcscis cosecantsecis secantcotis cotangent
Note that the ratios can be remembered using the mnemonic:
SOH-CAH-TOA
where:
Sine = Opposite ÷ Hypotenuse
Cosine = Adjacent ÷ Hypotenuse
Tangent = Opposite ÷ Adjacent
Plots of Trigonometric Functions
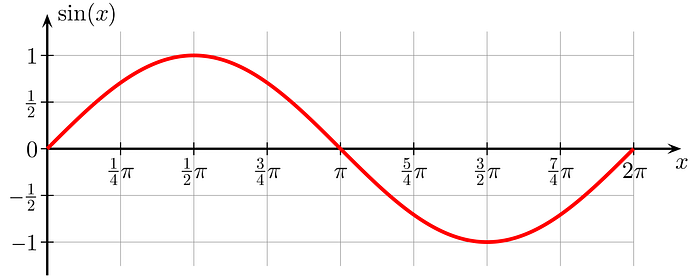
The plot of sin(x) is shown below:
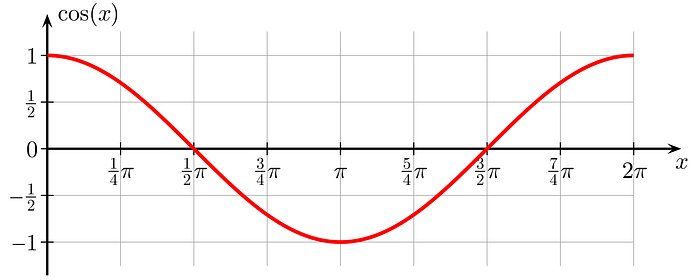
The plot of cos(x) is shown below:
Note that when we compare the plots of sin(x) and cos(x), they are at a phase difference of π.
This means that if we move the curve of cos(x) relative to sin(x) by π, both will overlap.
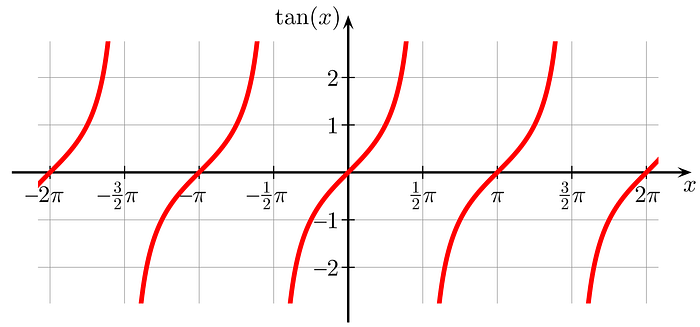
The plot of tan(x) is shown below:
Calculating Values of Trigonometric Functions
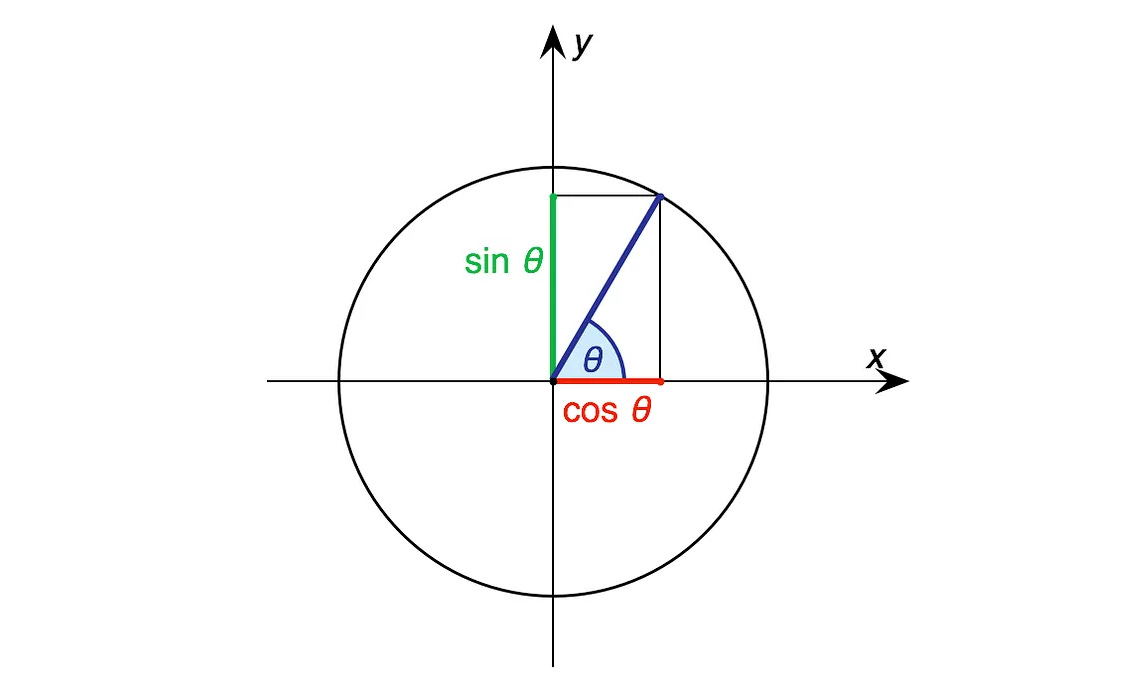
If we draw a right-angled triangle inside a circle of radius of unit length, the position of the point where the radius intersects the circumference of the circle can be represented by (x, y) where:
x = cos θ
y = sin θ
Values of trigonometric functions for different θs can be found by drawing a triangle inside a circle and calculating its ratios.
Radian
Angles, as described above, are commonly measured in Radians.
One radian is the angle subtended from the centre of a circle by an arc equal to the circle's radius.
2πradians =360°
1radian =57.2958°
Trigonometric identities
The following identities are Pythagoras Theorem in disguise.
Below-mentioned identities are Euler’s Formula in disguise.
If an angle
θcan be written as a sum or difference of two other anglesαandβi.e.θ = α ± β
I hope this article helped you grasp some Trigonometric concepts, as we will use them extensively in Quantum computing.
This list is not exhaustive but good enough to start with.
See you soon in the next part.





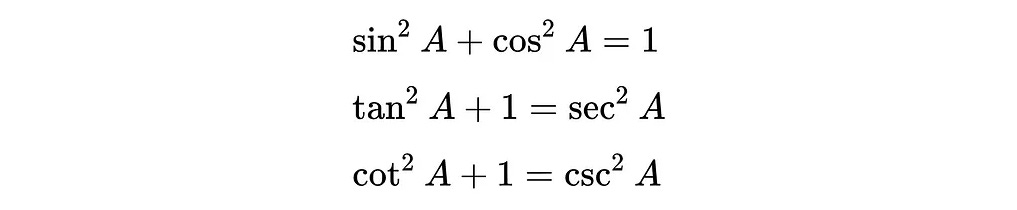
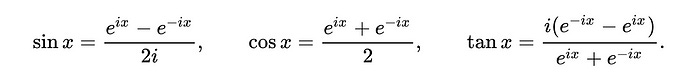
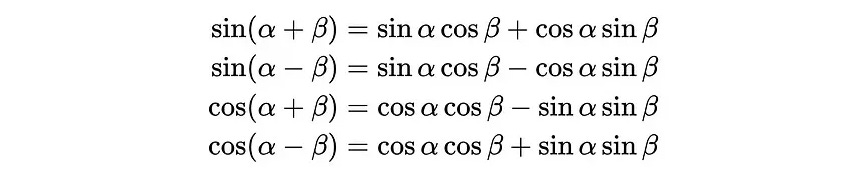

Nice overview. Reminds me of my own effort along these lines: https://logosconcarne.substack.com/p/easy-trigonometry