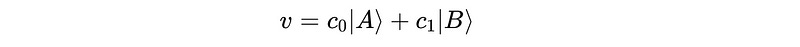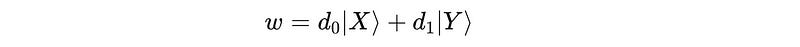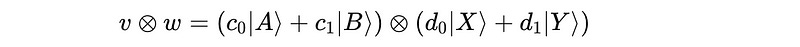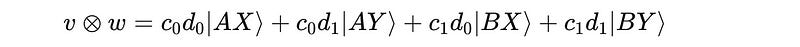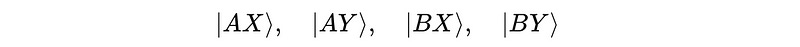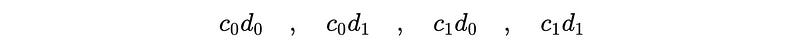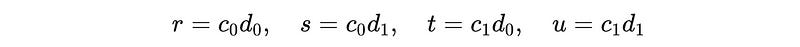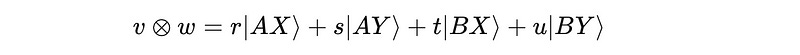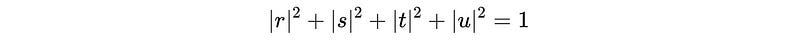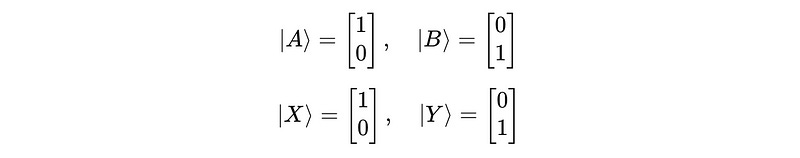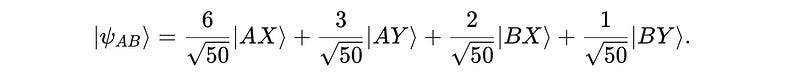The Mathematics Of Entangled Qubits

In this lesson, we learn all the mathematics behind Quantum Entanglement from the ground up.

Photograph of Erwin Schrödinger, a brilliant physicist best known for his wave equation and the thought experiment "Schrödinger's cat," which illustrates quantum superposition. Schrödinger also coined the term Verschränkung (German for entanglement) and recognized its fundamental role in quantum mechanics. (Image from Wikimedia Commons)

In the previous lessons, we learned how to work with single qubit systems that were represented with a ket vector.

But this is not all it.

A qubit can exist in a state where its properties can be affected by another qubit even when a vast distance separates them.

Such qubits are said to be “entangled”, and the phenomenon is known as Quantum Entanglement.

Let’s understand this better using some mathematics.

Let’s say that Alice has a qubit v as a superposition in the orthonormal basis vectors ∣A⟩ and ∣B⟩.

This qubit can be represented as follows:

The probability amplitudes of these basis vectors are represented by c(0) and c(1).

Similarly, another person, Bob, has a qubit w as a superposition in the orthonormal basis vectors ∣X⟩ and ∣Y⟩.

The probability amplitudes of these basis vectors are represented by d(0) and d(1).

The combined state of both the qubits can be represented using the tensor product between them.

This equation can be simplified further as:

What we see here is a two-qubit state which exists in a 4-dimensional Hilbert space with its orthonormal basis vectors being:

where the following represents the probability amplitudes of these basis vectors:

These can be denoted by:

This makes the original equation:

We know from the previous lessons that the square of these probability amplitudes will give the actual probability of finding this two-qubit system in these basis states.

This means that when Alice and Bob both measure their qubits, the probability of Alice finding her qubit in the state |A> and Bob in the state |X>, is given by c(0)² d(0)² or r² and so on.

Also:

---

The Standard Basis For A Two-Qubit System

Let’s say that both Alice and Bob were using the computational basis to measure their qubits, which are shown below:

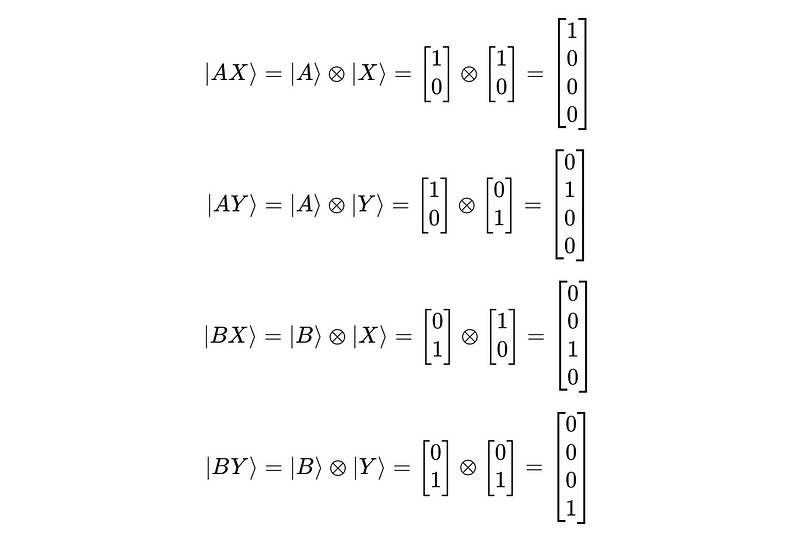
Then their tensor product gives:

This gives us the standard basis vectors for a two-qubit system in a four-dimensional Hilbert space:

---

Working With An Unentangled Two-Qubit System

Let’s start with a two-qubit state consisting of qubits from Alice and Bob, as follows:

Is it possible to separate the two qubits from Alice and Bob?