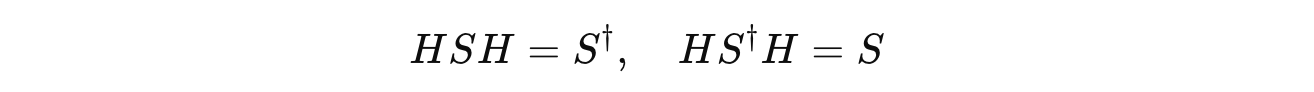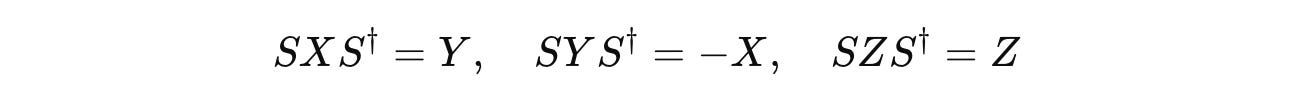Exploring 5 Important Single-Qubit Quantum Gate Relations
Did you know that HXH = Z and HZH = X?
In the last few weeks, we have discussed:
How quantum gates work and the mathematics behind them
What single-qubit quantum gates are and how they change the state of a qubit
How to use single-qubit quantum gates to build a quantum circuit
In this week’s lesson, we will learn about some interesting relations of single-qubit quantum gates that you can use when building quantum circuits.
Let’s begin!
1. General Form Of The Single-Qubit Quantum Gate
Any single-qubit quantum gate can be written as:
U denotes that the quantum gate is Unitary.
α is the Global Phase
θ controls the amplitude mixing between |0⟩ and |1⟩ states
ϕ controls the phase of the |0> → |1> transition amplitude
λ controls the phase of the |1> → |0> transition amplitude
This general form is mathematically the same as:
This is called ZYZ decomposition because it decomposes any single qubit gate into three sequence rotations: around the Z-axis, the Y-axis, and the Z-axis again.
2. Hadamard Conjugation Relations
These relations show how the Hadamard gate maps between the Pauli gates.
For the Phase gates S and S†, the relations are as follows:
3. Pauli Anti-Commutation Relations
We have previously learned that Pauli matrices anti-commute.
Some of the interesting relations this leads to are as follows:
4. S-Gate Conjugation Relations
We know that the S-gate introduces a 90° phase difference between |0⟩ and |1>, which corresponds to a rotation of π/2 radians around the Z-axis of the Bloch sphere.
It forms the following relations with the Pauli gates:
5. Exponential Relations
A Hadamard gate is its own inverse:
This is true for the Pauli gates as well:
For the S and T phase gates, they have the following relations:
That’s everything for this lesson.
To learn quantum computing is the best possible way, please derive/ prove these relations by hand, and use them to manipulate qubits on the Bloch sphere yourself.
Message me if you get stuck in the process and need any help.
Thanks for being a curious reader of “Into Quantum”, a publication that aims to teach Quantum Computing from the ground up.
See you soon in the next lesson!