A Deep Dive Into The Mathematics Of Quantum Gates
Understand Quantum gates like a pro by grokking the mathematics behind them.

You must be familiar with logic gates if you've been programming computers.
George Boole first introduced Boolean logic in the 19th century.
Claude Shannon later applied Boolean functions to electrical components as part of his master’s thesis, A Symbolic Analysis of Relay and Switching Circuits.
These logic gates NOT, AND, OR and their combinations are now ubiquitous and used to create all computational circuits in modern-day computers.
Similar to these, Quantum computers are formed using Quantum circuits composed of Quantum gates that manipulate qubits and perform computations.
Given a qubit, Quantum gates can perform the following operations:
Flipping qubit states
Creating Superposition
Introducing phase shifts
Entangling multiple qubits
To understand them better, we must deeply understand the mathematics behind them.
This lesson is all about that.
Quantum Gates Are Unitary Matrices
Mathematically, a quantum gate is a Unitary matrix.
This means that it is a square matrix whose conjugate transpose (Hermitian transpose) is its inverse.
For a unitary matrix U ,the following is true:
This means multiplying the matrix with its conjugate transpose returns the identity matrix.
How Does A Quantum Gate Act On A Qubit?
We know from the previous lessons that quantum states are unit vectors in 2^n-dimensional complex space (C^(2n)).
For example, a single qubit is represented as a unit vector in a two-dimensional complex space as a superposition of the computational basis states |0> and |1>.
Applying a quantum gate actually means the matrix multiplication of the gate with the qubit.
For a gate to act on n qubits, this gate has to be a 2^n x 2^n unitary matrix.
For example, a gate acting on a single qubit is a unitary matrix of dimension 2 x 2.
On the other hand, a multi-qubit system (also called a quantum register) of 2 qubits, represented by the tensor product of the constituent quantum states, will require a gate of dimension 4 x 4.
Why Are Quantum Gates Unitary?
Let’s begin with the basics.
A qubit |ψ> exists in the following superposition state in the Hilbert space:
where:
These are the computational basis states and α and β are probability amplitudes.
They satisfy the normalization equation as follows:
This means that the total probability of all possible outcomes obtained on measuring this qubit must be 1, or that all possible outcomes together must have a 100% chance of being measured.
When a quantum gate acts on a qubit, it transforms the qubit to |ψ'>:
This can be expanded to:
Even after applying the quantum gate, the new state must satisfy the normalization equation:
We know that the LHS is equal to the inner product of the state with itself (multiplication by its Hermitian or conjugate transpose (bra)):
And, for this state to be valid:
Going back to the equation that describes the application of the quantum gate:
Let’s multiply this state (ket) by its Hermitian or conjugate transpose (bra):
Since:
The equation becomes:
We know that the original state follows the normalization equation or
Therefore:
Thus, quantum gates must be Unitary to make this possible and follow the normalization equation, not violating the rules of quantum mechanics.
Unitarity Makes Quantum Gates Reversible
For any quantum gate represented by a Unitary matrix U, its operation can be reversed/ undone by applying U† (the gate’s Hermitian/ conjugate transpose):
This makes quantum gates always reversible.
This reversibility ensures that no information is lost while applying a quantum gate.
Unitarity Preserves Magnitude Of Quantum States
Unitarity guarantees that quantum gates preserve the magnitude (norm) of quantum states (as the overall norm remains the same, i.e. 1 after applying a quantum gate).
The following equation shows this norm:
Since we know that Unitary ensures that after applying a quantum gate, the total probability of the resulting state sums to 1:
This means that:
A single qubit’s state is represented as a point on the surface of the Bloch sphere.
Quantum gates act as rotations of this point around the sphere, changing the state vector’s orientation by modifying its relative phases and probability amplitudes.
However, they do not change the overall magnitude or its distance from the center, ensuring that the state vector does not shrink or stretch. As a result, the quantum state always stays on the surface of the Bloch sphere.
This is true for multi-qubit systems as well, but there is no simple sphere visualization, as these operations take place in an abstract 2^n-dimensional complex space.
Quantum Gates Represent The Time Evolution Operator
In quantum mechanics, the time-dependent Schrödinger equation describes how unmeasured quantum systems evolve over time.
For a quantum state |ψ(t)>, its time evolution is described as:
where:
His Hamiltonian, an operator that represents the total energy of a quantum systemħis the reduced Planck constant
Rearranging this equation:
And finally, solving it for a time-independent Hamiltonian or a constant H leads to:
This can be written as:
where U(t) is a unitary operator as follows:
You'd ask how this all relates to a Quantum gate.
Here is how: When a quantum gate, represented by the unitary operator U(t), is applied to a qubit, the qubit evolves from one state to another over a fixed time duration t as seen in the above equation.
A quantum gate represents this time evolution as per the principles of quantum mechanics.
Unitarity Allows The Stacking Of Quantum Gates
When two quantum gates U(1) and U(2) (that are unitary) are combined, their product U(1)U(2) is also unitary.
Mathematically, this is shown as follows:
This means that multiple quantum gates can be combined into complex circuits without breaking the laws of quantum mechanics.
This briefly explains what quantum gates are and what they do mathematically.
Thanks for being a curious reader of “Into Quantum”, a publication that aims to teach Quantum Computing from the very ground up.
See you soon in the next lesson!


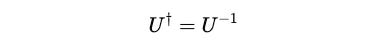
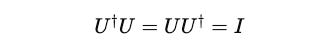
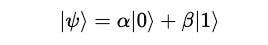
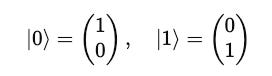
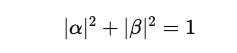
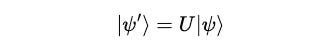
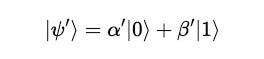
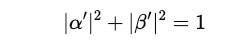
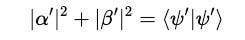
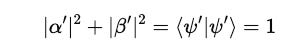
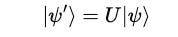
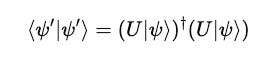
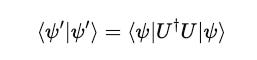
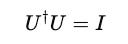
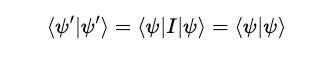
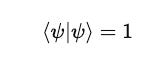
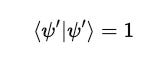
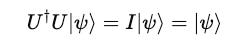
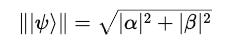
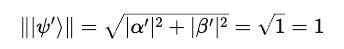

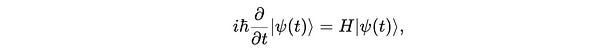
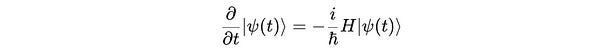
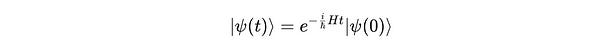
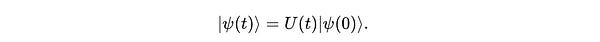
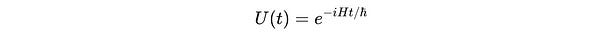
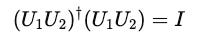

Nice post, and fun to see the Bloch sphere pop up. I just wrote about it earlier this month:
https://logosconcarne.substack.com/p/the-bloch-sphere