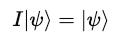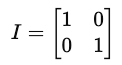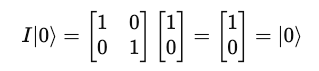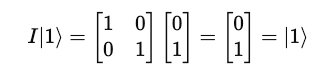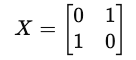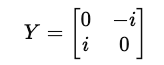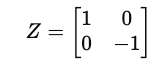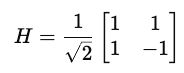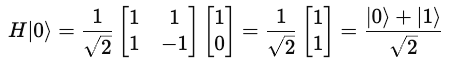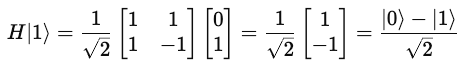A Lesson On Single-Qubit Quantum Gates (Part 1)
Learn about the Identity gate, Pauli gates and the Hadamard gate in this lesson.
We have previously discussed the mathematics behind Quantum gates in depth, which is an important lesson to take before this one.
This week’s lesson is all about single-qubit quantum gates.
Let’s begin!
What Are Single-Qubit Quantum Gates?
Single-qubit quantum gates act and operate on individual qubits to manipulate their quantum state.
Each quantum gate represents the rotation of a point representing a qubit on the Bloch sphere.
Since there are infinitely many possible rotation axes and each axis can have infinitely many rotation angles, the space of all possible operations on a qubit is uncountably infinite.
Therefore, there are uncountably infinite single-qubit gates.
Some of these gates are more commonly used and hence named. We will discuss these gates in more detail next.
1. Identity Gate
This gate, when applied to a qubit, preserves its state or leaves it unchanged.
where the Identity gate is represented by I and the following matrix:
It is represented by the following symbol in a quantum circuit diagram:
For example, I applied to |0> returns |0>.
And, I applied to |1> returns |1>.
2. Pauli Gates
There are three Pauli gates are follows:
X-gate: which causes a bit flip (like the classical NOT gate) for a qubit state
It is represented by the following symbols in a quantum circuit diagram:
or,
Y-gate: which causes a combination of a bit flip and a phase flip for a qubit state
It is represented by the following symbol in a quantum circuit diagram:
Z-gate: which causes a phase flip for a qubit in the state
|1>but leaves|0⟩unchanged.
It is represented by the following symbol in a quantum circuit diagram:
We have discussed these gates in a lot of depth previously. In case you missed it, this lesson can be found here.
3. Hadamard Gate
This gate is used to create a quantum superposition state.
It is represented by the following matrix:
It is represented by the following symbol in a quantum circuit diagram:
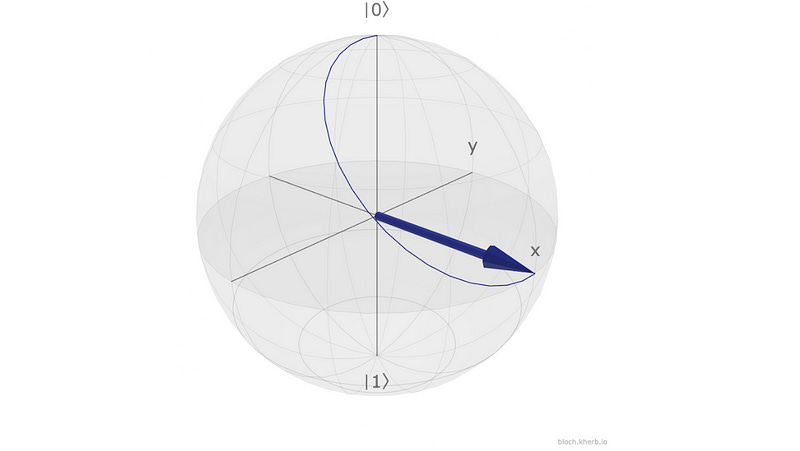
When H acts on |0>, it creates the following superposition state:
This looks as follows on the Bloch sphere:
And when H acts on |1>, it creates the following superposition state:
This looks as follows on the Bloch sphere:
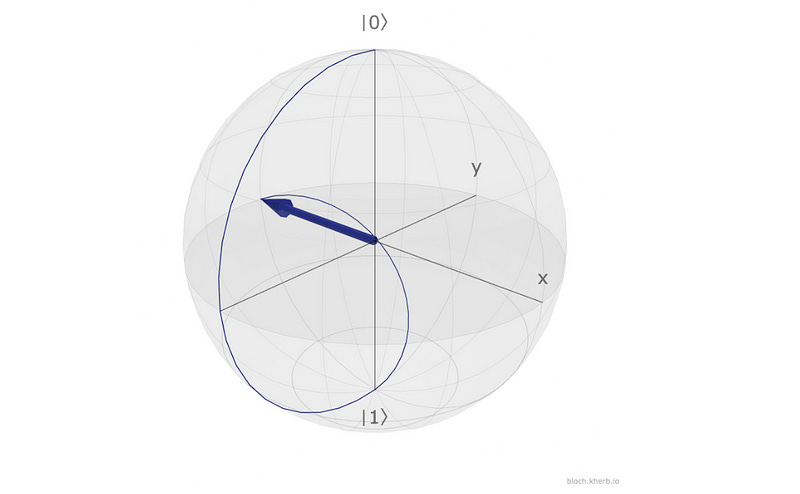
The resulting states are equal superposition states with opposite relative phases or a relative phase difference of π.
We have previously discussed applying the Hadamard gate to build a quantum circuit on a real quantum computer.
In case you missed this lesson, it can be found here.
This lesson on single-qubit gates is divided into multiple parts to keep it short and easy to grasp.
Thanks for being a curious reader of “Into Quantum”, a publication that aims to teach Quantum Computing from the very ground up.
See you soon in the next lesson!