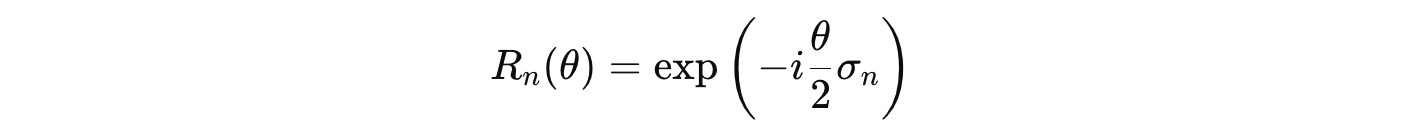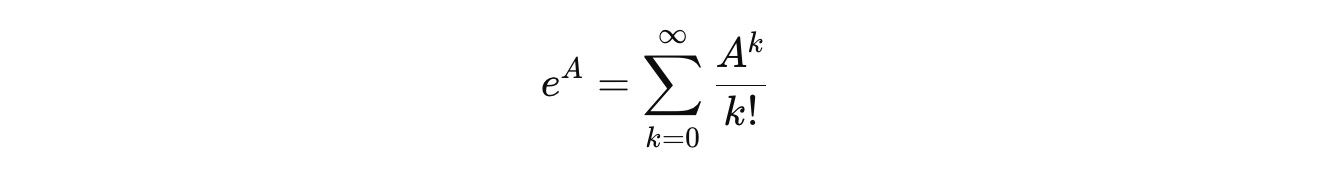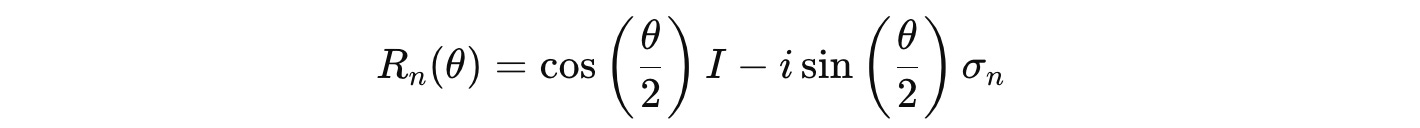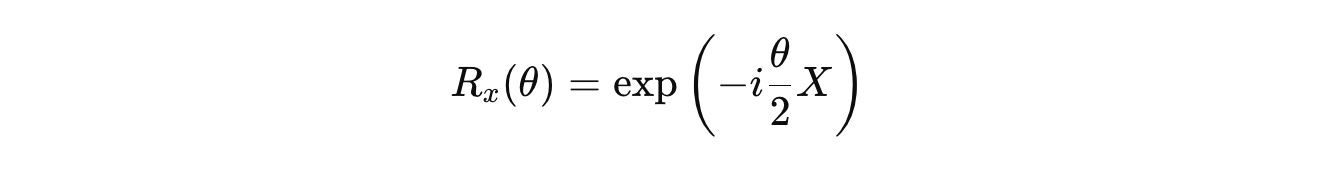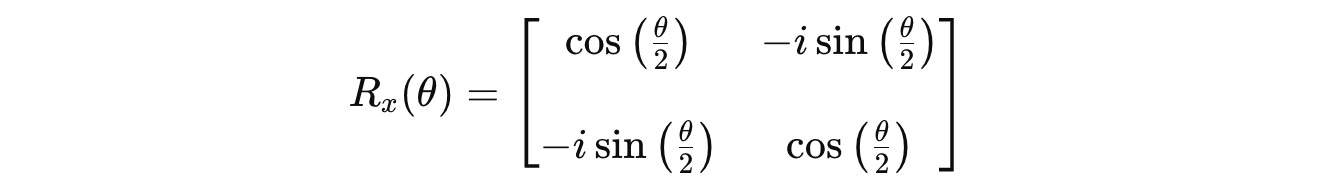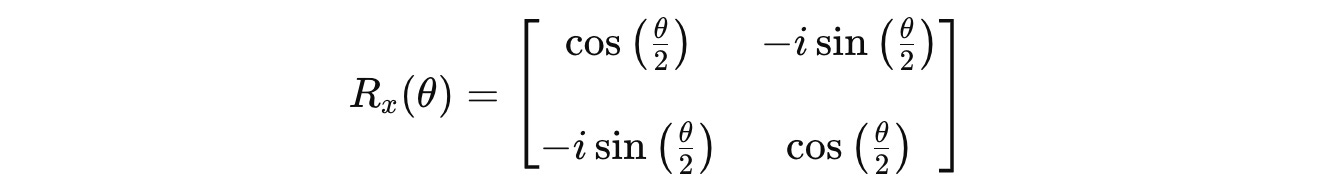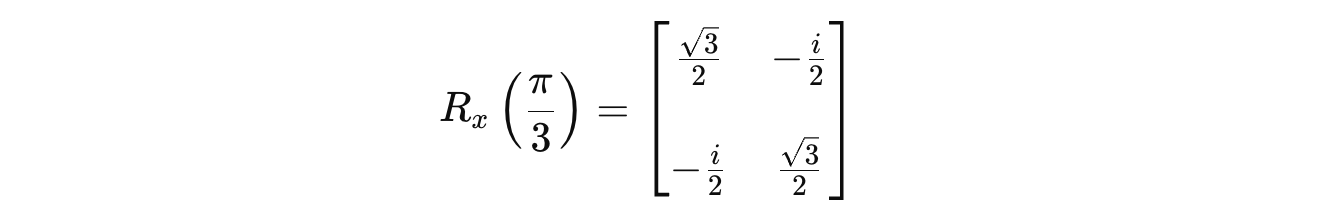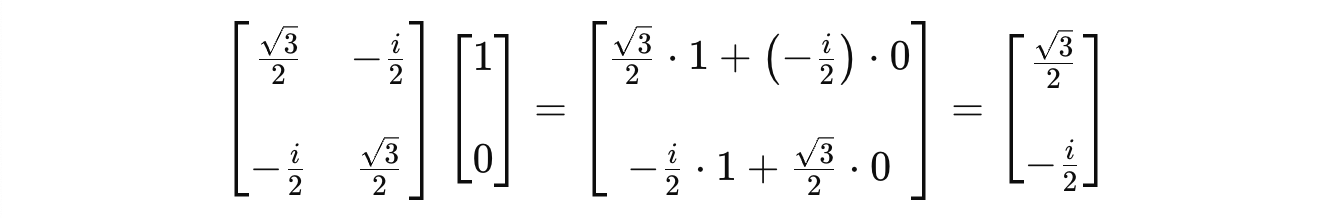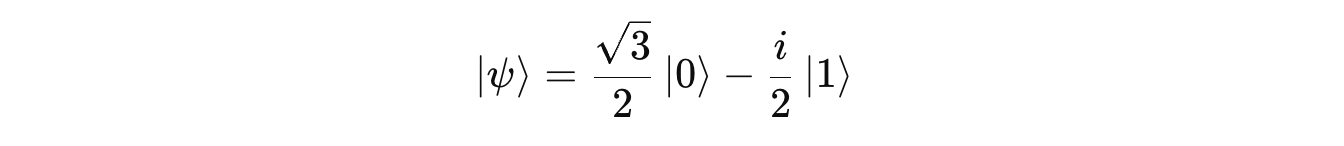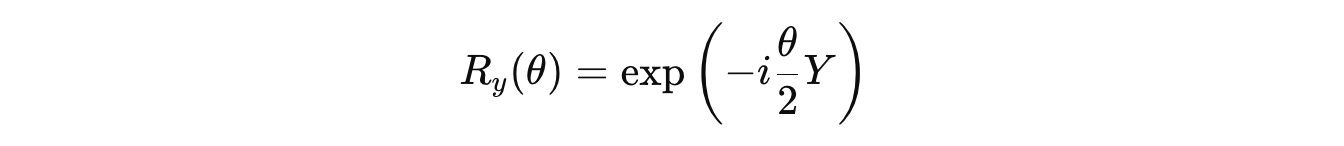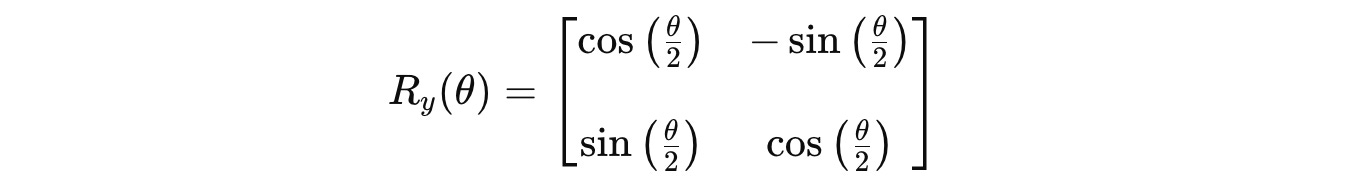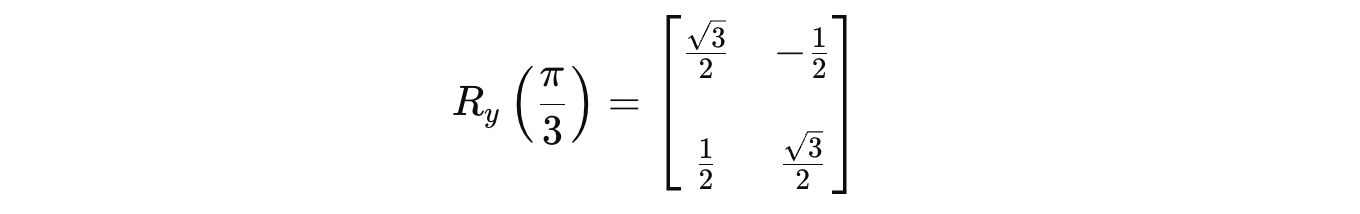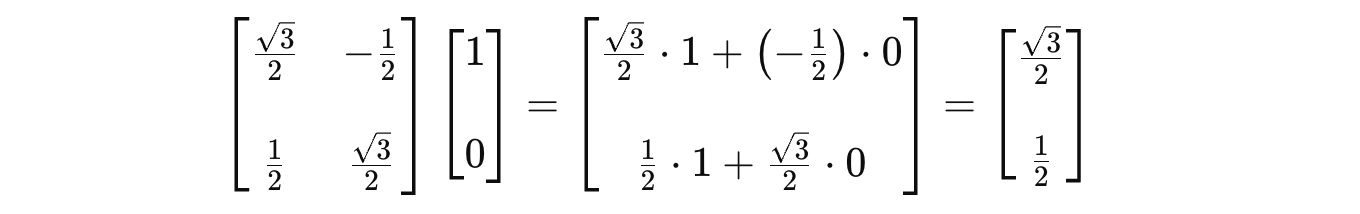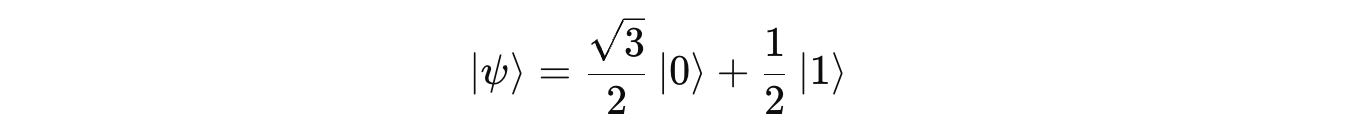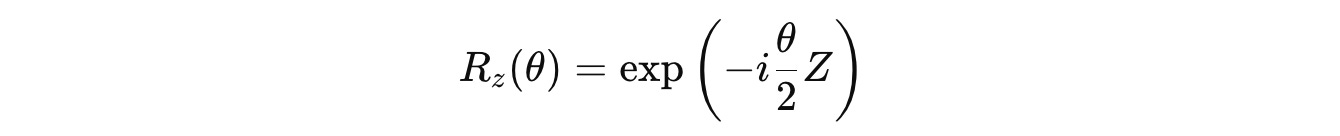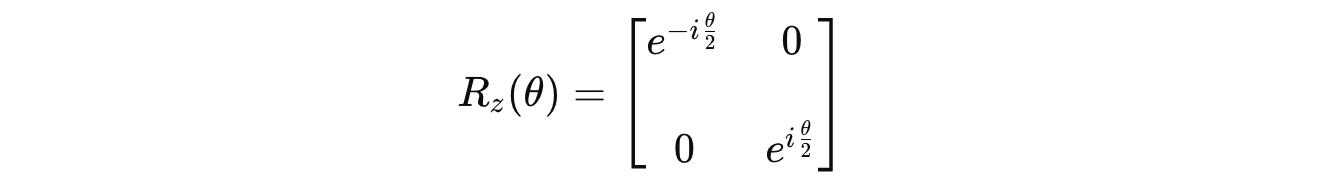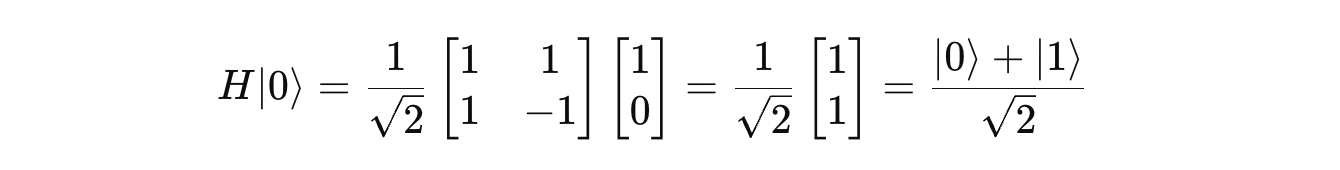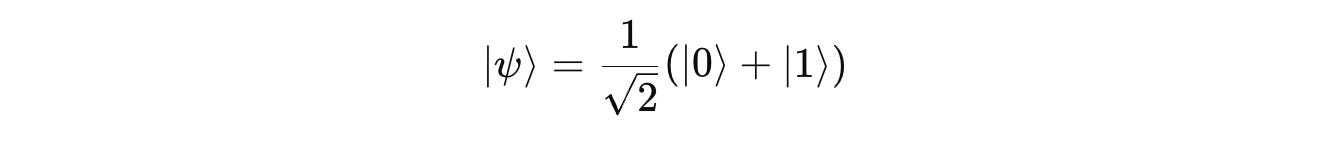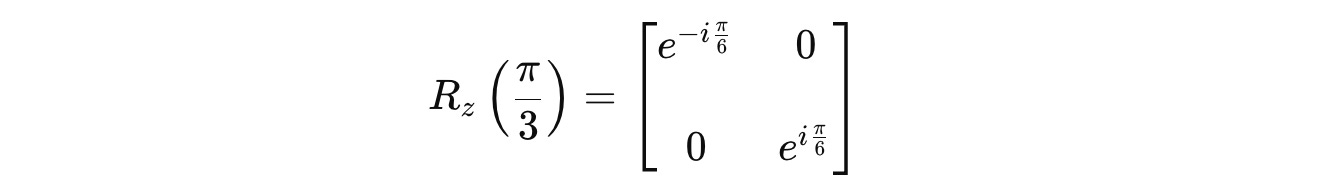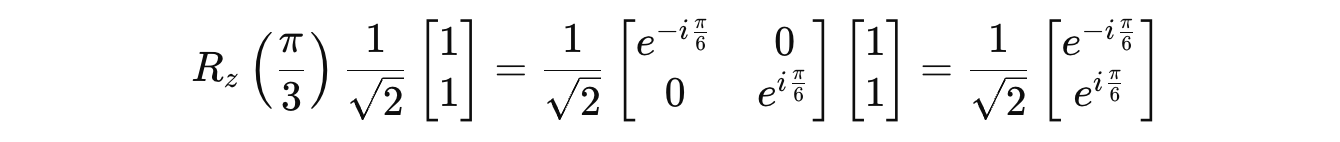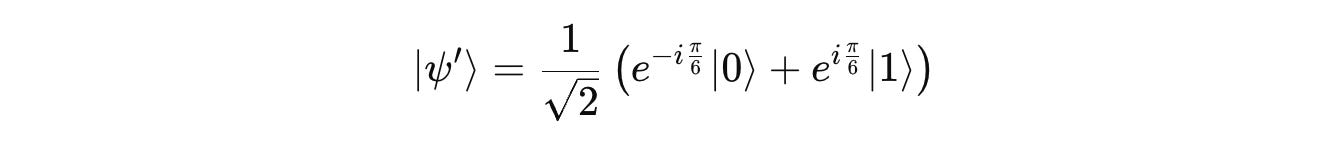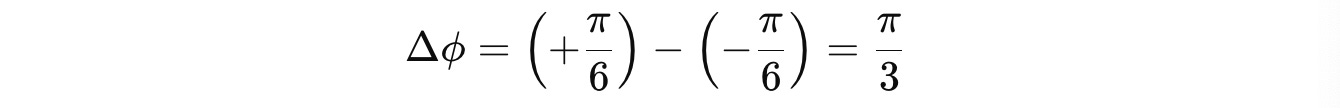A Lesson On Single-Qubit Quantum Gates (Part 3)
Learn all about Rotation gates used in Quantum computing in this lesson.
We discussed Quantum Phase gates in last week’s lesson.
This week, we will move forward to learn about Rotation gates.
In case you missed the previous lessons on Quantum gates, here are the links for them:
Let’s get started!
5. Rotation Gates
These are single-qubit quantum gates that change a qubit’s state by performing rotations around specific axes of the Bloch sphere.
The following equation represents the exponential form of a rotation gate:
Using the Taylor series for the exponential of a matrix:
This can be further simplified to:
where:
θ is the rotation angle
σ(n) represents a Pauli matrix
I is the Identity matrix
There are three important rotation gates, each corresponding to a rotation around one of the axes (X, Y, or Z).
R(x)(θ): for rotation around the X-axis
R(y)(θ): for rotation around the Y-axis
R(z)(θ): for rotation around the Z-axis
Let’s study them in detail.
R(x)(θ) gate
This gate causes a qubit state to rotate around the X-axis of the Bloch sphere by an angle θ (in radians).
It is represented as follows in the exponential form, where X is the Pauli-X matrix:
On further derivation using the above equation, the gate is represented using the following square matrix:
It is represented by the following symbol in a quantum circuit diagram:
Let’s take an example where we apply this gate to rotate a qubit originally in state |0> by 60 degrees, or π/3 radians.
The matrix for the R(x)(π/3) gate is as follows:
This applied to the qubit is state |0> results in:
This is a superposition with 75% probability of obtaining |0> and 25% probability of obtaining |1> when a measurement is done.
The rotation is shown on the Bloch sphere in the following image.
R(y)(θ) gate
This gate causes a qubit state to rotate around the Y-axis of the Bloch sphere by an angle θ (in radians).
It is represented as follows in the exponential form, where Y is the Pauli-Y matrix:
On further derivation using the above equation, the gate is represented using the following square matrix:
It is represented by the following symbol in a quantum circuit diagram:
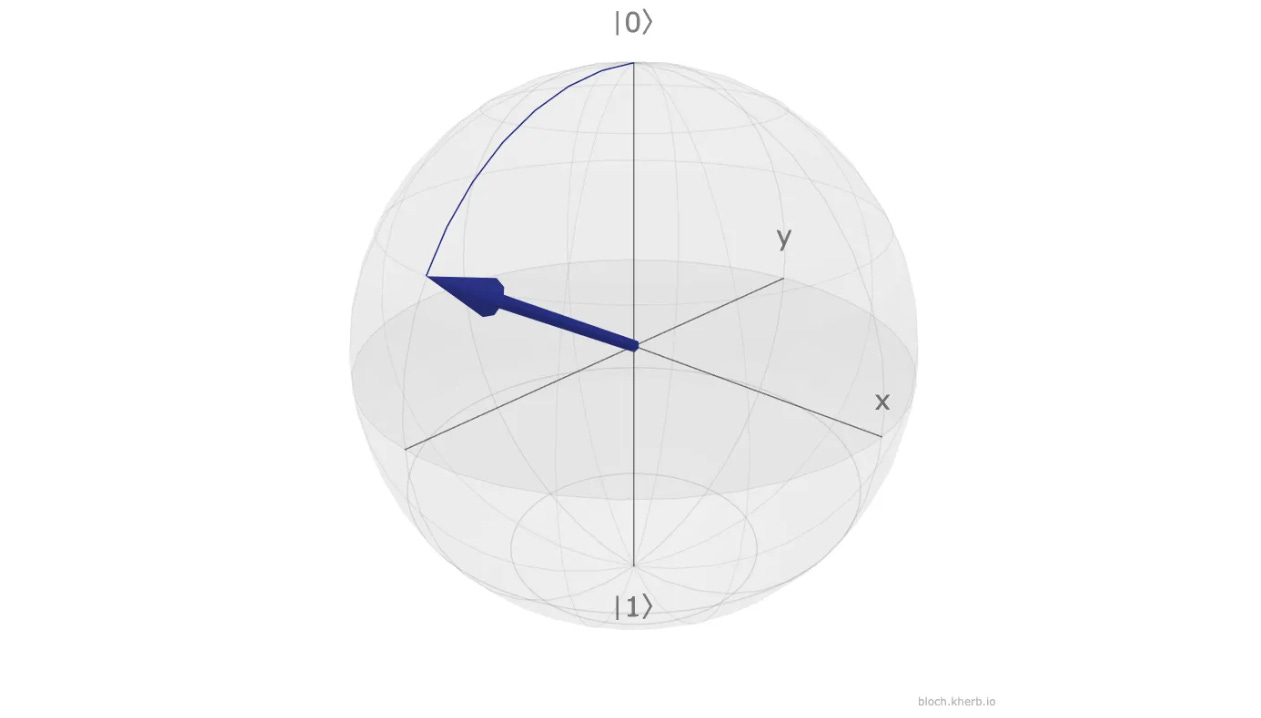
Let’s take an example where we apply this gate to rotate a qubit originally in state |0> by 60 degrees, or π/3 radians.
The matrix for the R(y)(π/3) gate is as follows:
This applied to the qubit is state |0> results in:
This is a superposition with 75% probability of obtaining |0> and 25% probability of obtaining |1> when a measurement is done.
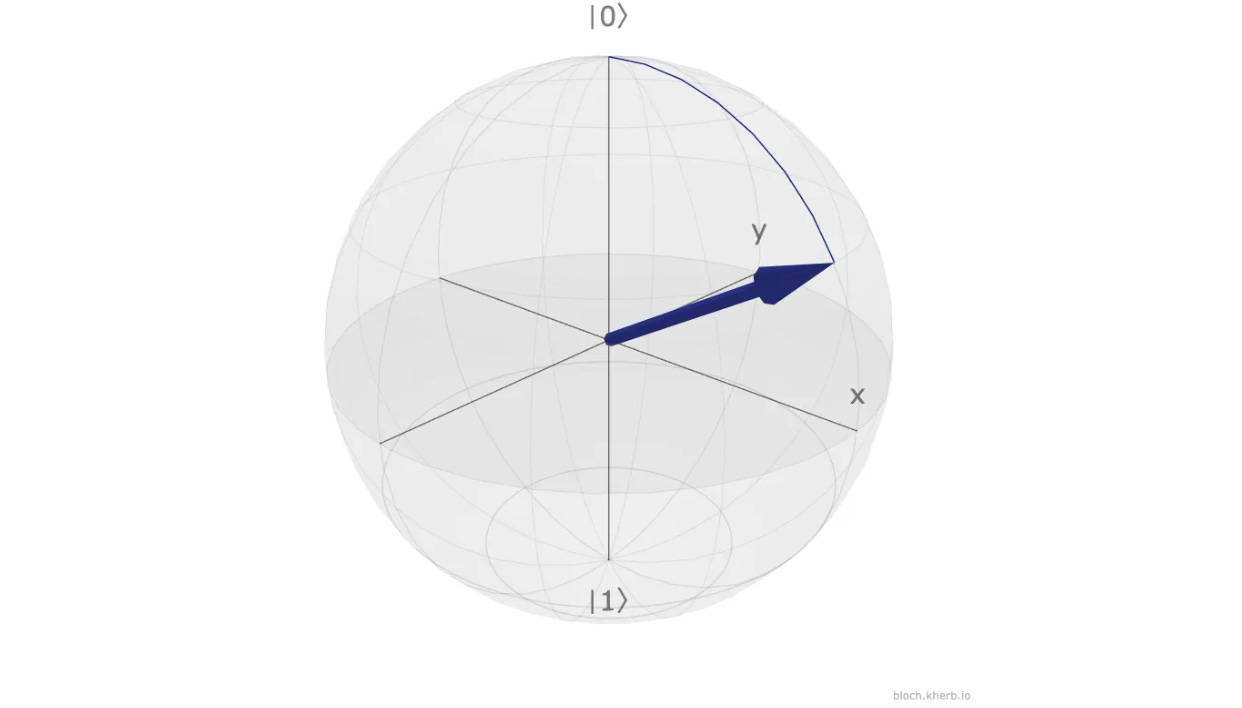
This is shown on the Bloch sphere in the following image.
R(z)(θ) gate
This gate causes a qubit state to rotate around the Z-axis of the Bloch sphere by an angle θ (in radians).
It is represented as follows in the exponential form, where Z is the Pauli-Z matrix:
On further derivation using the above equation, the gate is represented using the following square matrix:
It is represented by the following symbol in a quantum circuit diagram:
Let’s take an example where we start with a qubit in an equal superposition state prepared by applying the Hadamard gate to |0>:
The resulting equal superposition state is:
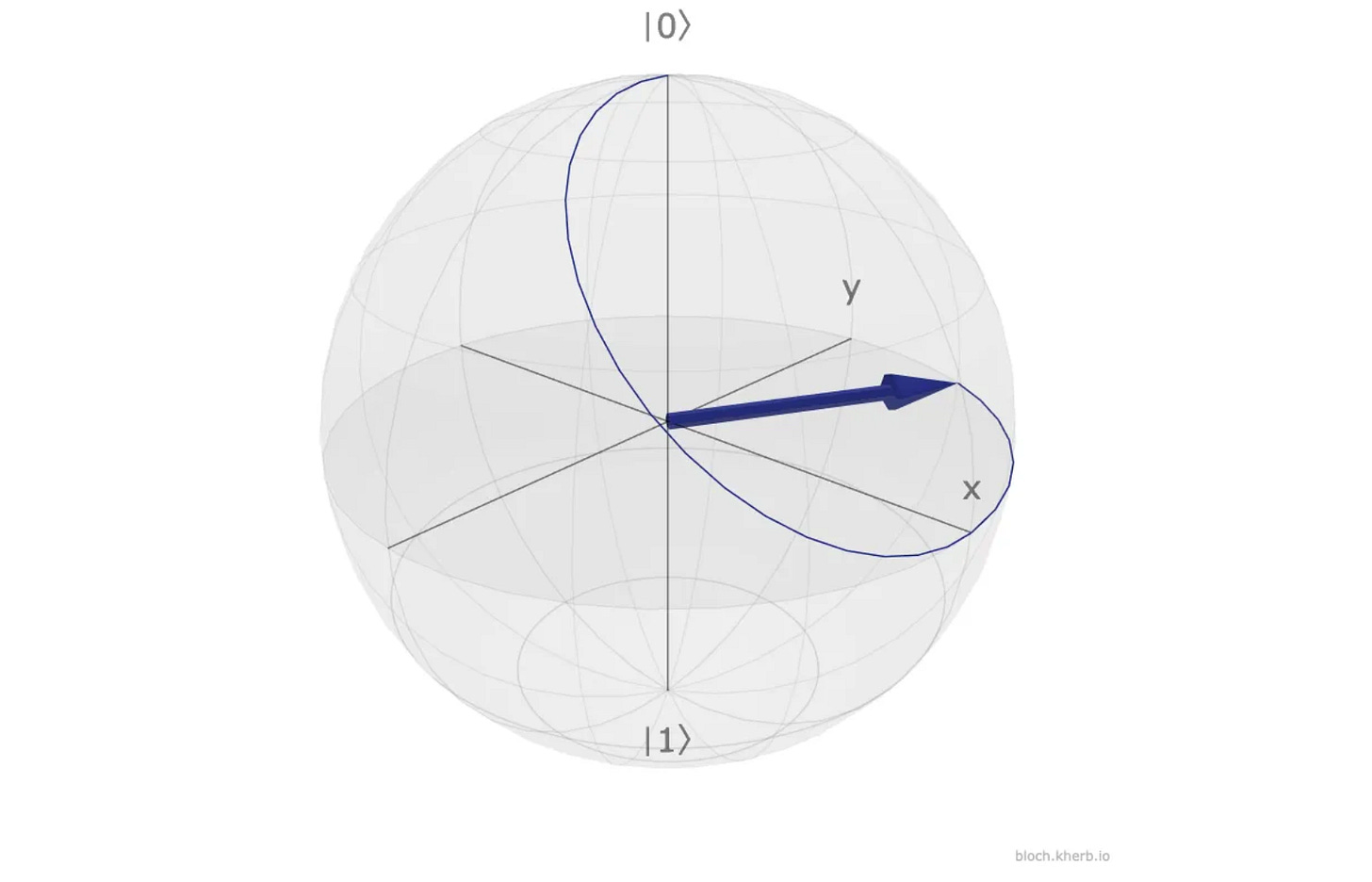
Next, we prepare the R(z)(π/3) gate that rotates this qubit by 60 degrees, or π/3 radians:
Applying this gate to |ψ> results in:
This is a superposition with a 50% probability of obtaining |0> and a 50% probability of obtaining |1> when a measurement is done.
The state has a relative phase of π/3 between |0> and |1>.
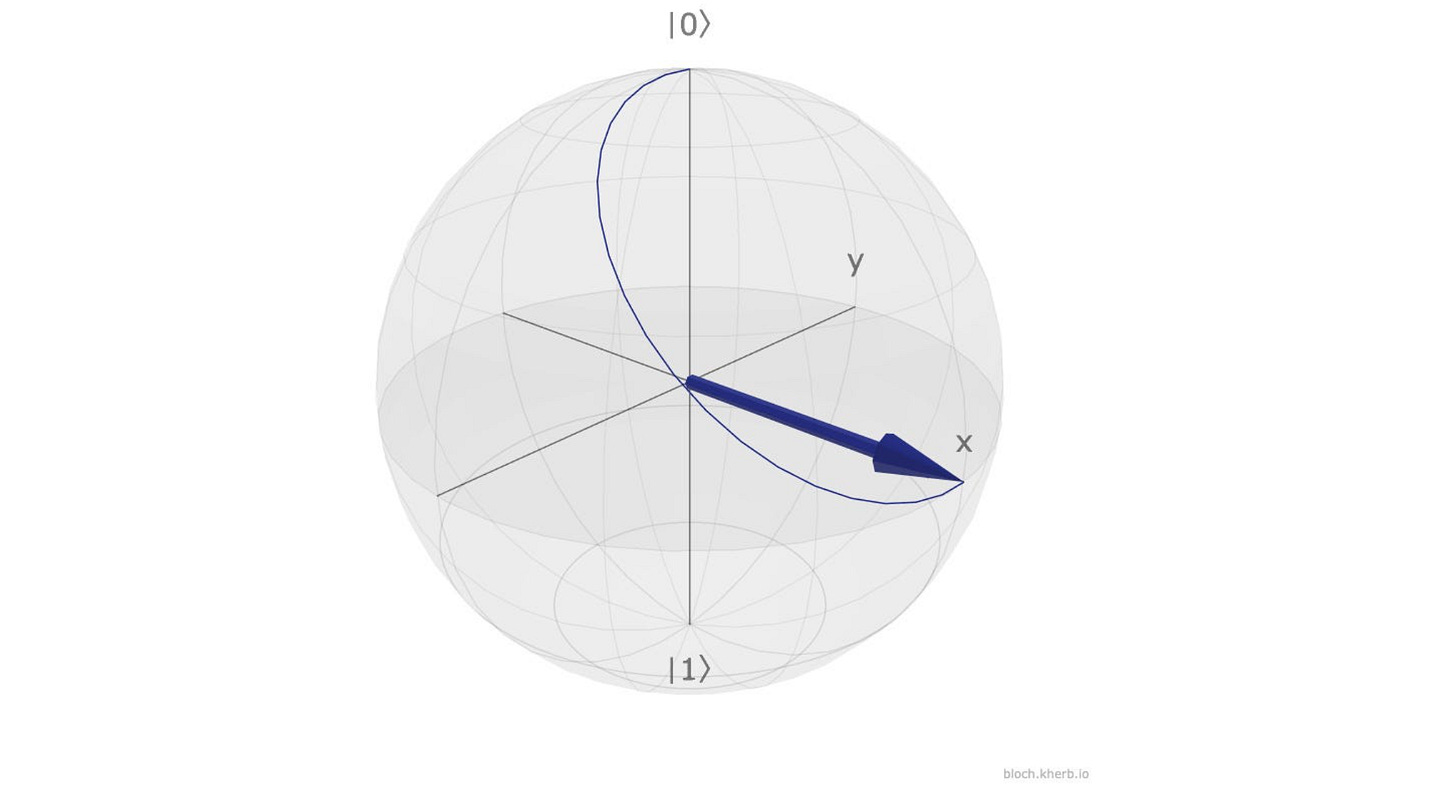
The above rotations are shown on the Bloch sphere in the following image.
Note that the R(z)(θ) gate always causes a relative phase change, and never changes the amplitudes. This means that the measurement probabilities of the qubit on the computational basis stay the same after applying the R(z)(θ) gate.
This is different from the R(x)(θ) and R(y)(θ) gates that change the amplitudes and measurement probabilities.
I would highly recommend applying Quantum gates on qubits and rotating them on the Bloch sphere yourself.
I’ve used bloch.kherb.io for this, and all the images in the articles are generated using this website.
Similarly, performing all matrix multiplication by hand will help you deeply understand this topic.
This lesson on single-qubit gates is divided into multiple parts to keep it short and easy to grasp.
Thanks for being a curious reader of “Into Quantum”, a publication that aims to teach Quantum Computing from the ground up.
See you soon in the next lesson!