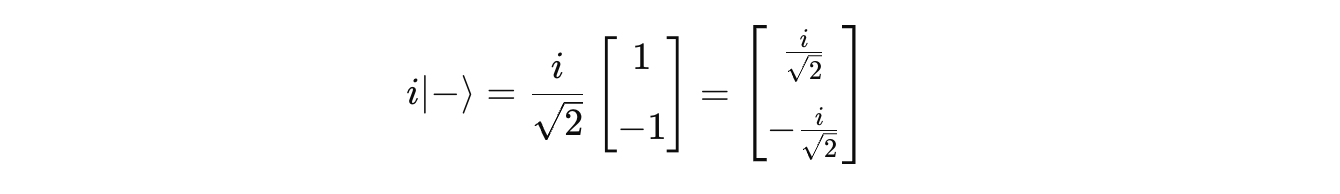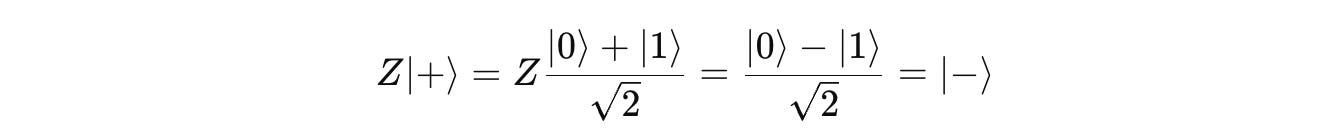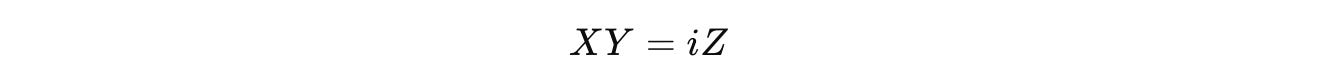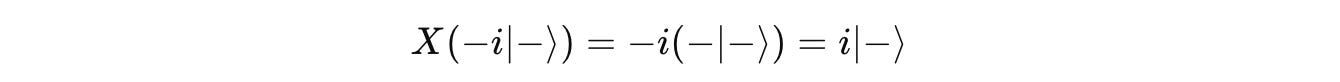Quantum Lego: Building States Using Quantum Gates

Solution to Question 4 of the ongoing Quantum programming challenge.

Hey everyone!

I recently published a challenge with 6 Qiskit questions to get started with Quantum Computing.

6 Qiskit Questions to Get Started with Quantum Computing

Here is the solution to the fourth question from the challenge.

---

Before we move forward, I want to introduce you to the Visual Tech Bundle.

It is a collection of visual guides that explain core AI, LLM, Systems design, and Computer science concepts via image-first lessons.

Others are already loving these books.

This includes Dharmesh Shah, the co-founder and CEO of HubSpot.

Dharmesh’s reply to my LinkedIn post. (Source)

Why not give them a try?

Now back to our lesson!

---

Question 4

Find the sequence of X, Y, and Z gates that transforms the quantum state |+⟩ to i|-⟩ . Verify the results using a Qiskit simulator.

---

Solution 4

|+> and |-> can be written as follows:

And, our target i|-> can be written as:

We know from previous lessons that the Pauli-Z gate causes a phase flip for a qubit in the state |1> but leaves |0⟩ unchanged.

Applying Pauli-Z to |+> results in:

From here, to get i|->, we can simply multiply both sides by i as follows:

Note the iZ term on the LHS. We know from a previous lesson on Quantum gate relations, that:

To apply XY to a state, the circuit must do:

• Apply Y first

• Then apply X

(Read it again!)

Following this, applying Pauli-Y to |+> results in:

Next, applying Pauli-X to this state results in our desired state.

---

Verifying the Result with a Quantum Simulator

Here is a program that checks whether our results are correct using the Qiskit simulator.

We start by importing the necessary libraries.

from qiskit import QuantumCircuit
from qiskit.quantum_info import Statevector
import numpy as np

Next, we create a quantum circuit with one qubit and apply our gate sequence.

The Hadamard gate (H) creates the |+> state from the default |0> state, which is followed by applying the Y and X gates.

# Create circuit
circuit = QuantumCircuit(1)

circuit.h(0)   # Convert |0> to |+>
circuit.y(0)   # Apply Y
circuit.x(0)   # Apply X

We can visualize the circuit as follows.

# Visualise the circuit
print(circuit)

"""
Output:
   ┌───┐┌───┐┌───┐
q: ┤ H ├┤ Y ├┤ X ├
   └───┘└───┘└───┘
"""

Next, we use the Statevector class to simulate the circuit and compute the final quantum state after all gates have been applied.

sv = Statevector(circuit)
print(sv)

"""
Output:
Statevector([0.+0.70710678j, 0.-0.70710678j],
            dims=(2,))
"""

In the final step, we manually define our target state i|-> and compare it against the simulation result.

target = np.array([1j/np.sqrt(2), -1j/np.sqrt(2)]) # |->
print("Target:", target)

"""
Output: 
Target: [ 0.+0.70710678j -0.-0.70710678j]
"""

print("Result matches the target") if np.allclose(sv.data, target) else print("Result does not match the target")

"""
Output:
Result matches the target
"""

The simulation confirms that applying the gate sequence Pauli-Y followed by Pauli-X to the state |+> successfully produces the target state i|->.

---

That’s everything for this article.

Thanks for being a curious reader of ‘Into Quantum’, a publication that teaches essential concepts in Quantum Computing from the ground up.

To get even more value from this publication, consider becoming a paid subscriber.