All The Math That You Need To Start Doing Quantum Computing (Part-1)
Lesson 1: Imaginary and Complex Numbers

We are living in an exciting era.
Google’s new AI chip, Willow, cracked a key challenge in quantum error correction that the field has pursued for almost 30 years.
With its state-of-the-art capabilities, it performed a standard benchmark computation in under five minutes that would take one of today’s fastest supercomputers ten septillion (that is, 10^25) years — a number that is bigger than the age of the Universe!
Quantum computing today is like AI in the 2000s.
Only a bunch of smart people understand it. But it is going to get big pretty soon.
This publication is here to teach all the fundamentals of Quantum Computing so that you are ready to be a part of this revolution when the right time comes.
Let’s Start With Quantum Computers
Quantum computers are machines that use the properties of quantum physics to store data and perform computations.
Instead of classical bits, Qubits (quantum bits) represent information in quantum computers.
These computers work on the principles of Quantum Mechanics, and one must know its basics to start with quantum computing.
How Is Quantum Mechanics Different From Classical Physics?
You must have read about Newton’s laws of motion, an important part of classical physics.
Classical Physics or Classical Mechanics is highly intuitive.
Throwing a ball and watching it follow a Parabolic path makes sense.
Quantum Mechanics is quite different from this.
As we reduce the size of objects we are interested in studying to levels of the size of an electron, we enter a fascinating, non-intuitive realm of reality.
To understand how things work here, we need to learn a whole new way of thought processes and logic.
This is what Quantum Mechanics aims to do.
This branch of physics uses abstract mathematics to comprehend the phenomenon ‘observed’ (so classical mechanics!) in the quantum world.
This series introduces all the mathematics you must understand to start doing quantum mechanics and quantum computing.
Lesson 1: Imaginary & Complex Numbers
The state of a Qubit is represented by complex numbers.
An Imaginary number is a real number (R) multiplied by i(the imaginary unit or iota).
i² = -1ori = √-1
Also,
i³ = -ii⁴ = +1i^(4n-1)= -i
(Don’t try calculating the square root of -1, it is imaginary for a reason!)
Examples of imaginary numbers are 2i, -5i, 0.3i, (4/5)i
A Complex number (z) is a sum of a real number and an imaginary number.
z = x + iy
where x and y are real numbers.
Conjugate of a Complex Number
Each complex number has a unique conjugate (or complex conjugate because it is a complex number) represented by z*.
It is the original complex number with its imaginary part of the same magnitude but an opposite sign.
For z = x + iy:
z* = x — iy
Addition of Complex Numbers
Two complex numbers can be simply added following the rules of arithmetic.
For x = a+ib and y = c+id:
x + y = (a+c) + i(b+d)
Subtraction of Complex Numbers
Two complex numbers can be subtracted following the arithmetic rules below.
x — y = (a-c) + i(b-d)
Multiplication of Complex Numbers
This operation is done using the identity (a+b)*(c+d) = a*c + a*d + b*c + b*d
x * y or (a+ib) * (c+id) = ac + ibc + iad + i²(bd)
Therefore,
x * y = (ac — bd) + i(bc + ad)
Multiplication of Complex Numbers with its Conjugate
This operation i.e. z * (z*) always results in a positive real number.
For x = a + ib, and its conjugate x* = a — ib,
x * (x*) = a*a — b*(-b) + i(b*a + a*(-b))
x * (x*) = a² + b²
Division of Complex Numbers
For x and y as above, x/y is performed by multiplying both the numerator and denominator by the conjugate of y.
x/y = (a + ib) / (c + id) = (a + ib)(c — id) / (c+id)(c-id)
This results in:
x/y = [(ac+bd)+ i(bc-ad)] /(c² + d²)
Representation of Complex Numbers
Complex numbers can be represented in two forms:
on the Cartesian plane (also called Argand Diagram/ Complex plane/ S-plane/ Gauss plane)
using Polar coordinates
Representation on the Cartesian/ Complex Plane
When a complex number is represented on a 2D Cartesian plane,
the vertical (y) axis corresponds to the imaginary part of the complex number
the horizontal (x) axis corresponds to the real part of the complex number

Representation using Polar Coordinates in the Polar Complex Plane
The Polar coordinate system is a 2D plane in which the position of a point is determined by a distance (called radius) from a reference point (called pole) and an angle from the reference direction (called polar axis).
Angles in polar notation are expressed in degrees or radians.
Note that
2π radians = 360°

A complex number can be represented in a Polar complex plane where the x-axis represents the real part, and the y-axis represents the imaginary part of a complex number.
A complex number z can be written using polar notation as:
where:
eis Euler’s numberφis called the argument of the complex numberzris called the absolute value/ modulus /magnitude of the complex numberz
Using the Pythagoras’ theorem,
If you got a bit confused up there, note that the above notation of representing a complex number uses Euler’s formula that states that for any real number x:
The graphical representation of this formula is shown below.
Let’s learn a few mathematical operations on complex numbers written in polar form.
(Note that addition and subtraction are easier in the non-polar/ component/ rectangular form, but multiplying and dividing are easier in the polar notation.)
Multiplication of Complex Numbers in Polar Representation
For two numbers z(1) and z(2) where:
The multiplication operation is done as follows:
or,
Division of Complex Numbers in Polar Representation
Similarly, the division operation is done as follows:
or,
I hope this article helped you grasp Complex numbers, as we will use them extensively in Quantum computing.
See you soon in the next part.








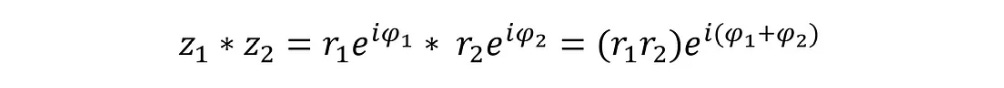




Would love your thoughts on my primer to quantum and explaining Willow!
https://open.substack.com/pub/matthewharris/p/willow?r=298d1j&utm_medium=ios
(I was always wanting to learn Quantum Physics but was really lost on what to and learn and where from!
This newsletter is a fantastic resource for me to begin my journey sir, thank you from a graduate student who just began learning because of your newsletter ☺️✨