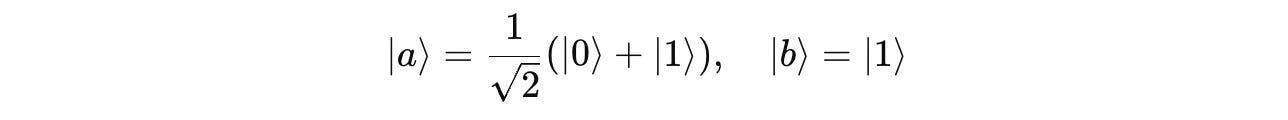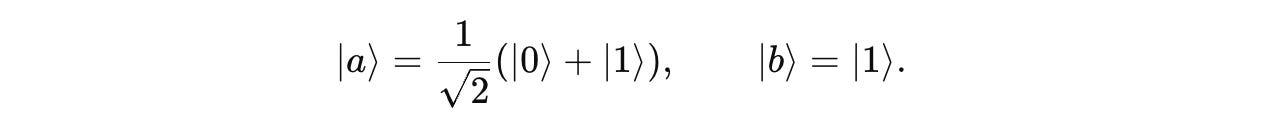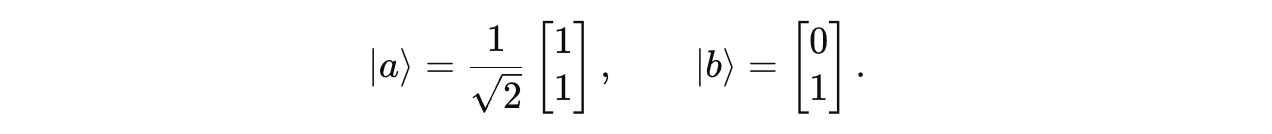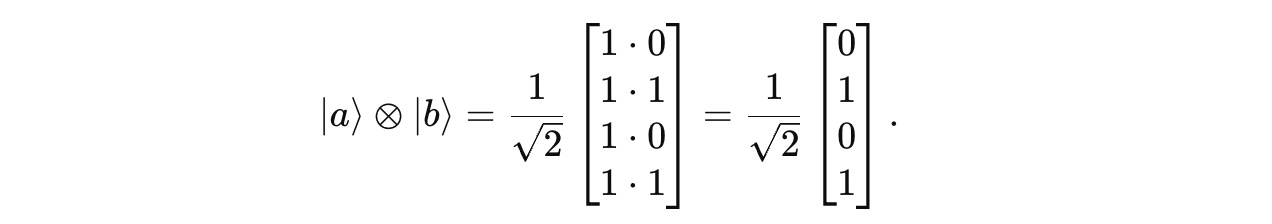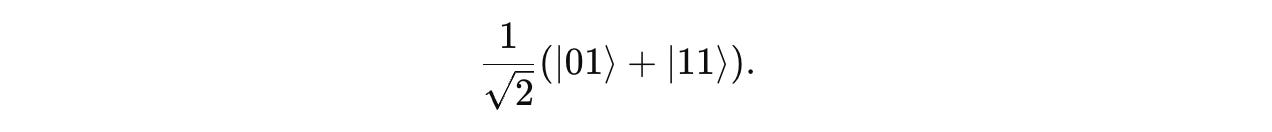How To Find The Tensor Product Of Two Qubits
Solution to Question 2 of last week's quantum challenge.

In the last post, I challenged you with six questions to help you strengthen the mathematical concepts that you need to master Quantum computing.
Let’s move on to the second question and solve it step by step using everything we have learned previously.
The question goes like this:
Given two qubits in the following states:
Find the tensor product between these states and express the result in the computational basis.
Tensor Product Of Two Qubits
We know from previous lessons that the tensor product of two vectors/ matrices combines them into a larger matrix.
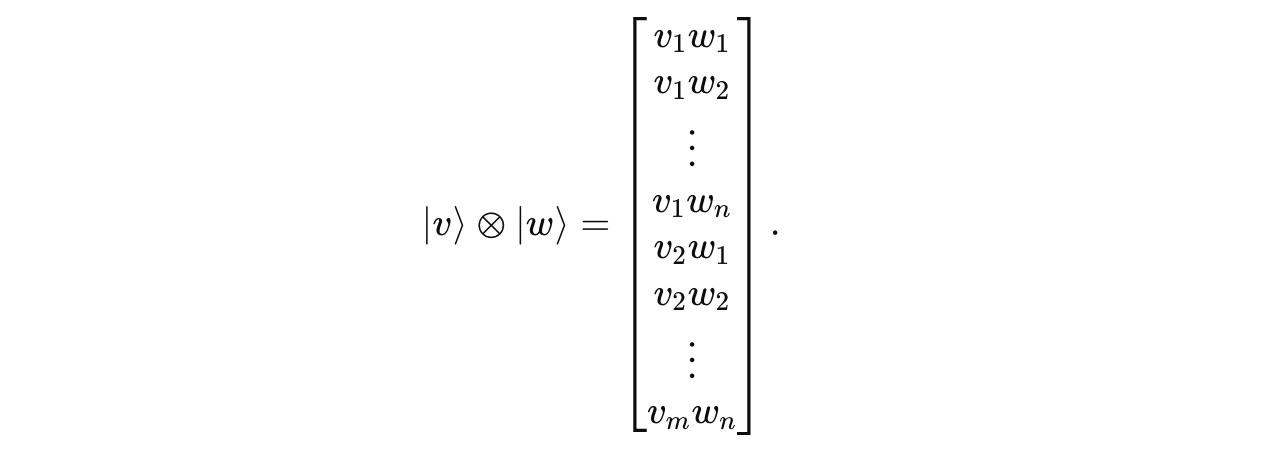
For two ket vectors:
Their tensor product is:
The given states |a> and |b> are on the computational basis as follows.
And they can be written in the vector form as follows.
Next, the tensor product between them is calculated as:
This result, on the computational basis for a system of two qubits, which is a set of four orthonormal states {|00>, |01>, |10>, |11>}, is written as follows:
I hope that you were able to solve this question by hand. See you soon in the next lesson!