Revisiting The Mathematics Of Quantum Computing
6 questions to grok the mathematics of Quantum Computing.
Most concepts in Quantum mechanics aren’t intuitive and might not have macroscopic world alternatives to rely on.
For example, in the macroscopic world, observing a car does not alter its state, but in the quantum world, observing a particle does change it.
This is the reason why Quantum phenomena are best described using mathematics, rather than English.
If you’re new to this publication, I would highly recommend learning about Quantum Mechanics/ Computing from a mathematical lens.
This week, we will revisit the mathematics of Quantum Computing and solidify our understanding of it through 6 questions.
I would love it if you could solve these by hand. I will reveal detailed solutions to them in the next post on this publication.
Let’s begin!
Question 1: Normalization
A single qubit is in the state:
where α = 5/ 3 and β = 4(i)/ 5.
Verify if this is a valid quantum state by showing that it is normalized.
Question 2: Tensor Product of Qubits
Given two qubits in the following states:
Find the tensor product between these states and express the result in the computational basis.
Question 3: Inner Product of Qubits
Given two qubits in the following states:
Find their inner product and tell whether the two states are orthogonal.
Question 4: Probability Amplitudes in Quantum Measurement
Given a qubit in the following state:
If this qubit is measured in the computational basis, what is the probability of observing |0>?
Question 5: Eigenvalues of the Pauli-Y Operator
The Pauli-Y operator is defined as:
Find its eigenvalues and corresponding normalized eigenvectors.
Question 6: Measurement Probabilities in a Rotated Basis
Given a qubit in the following state:
If we measure it in the Hadamard basis, what is the probability of obtaining |+>?




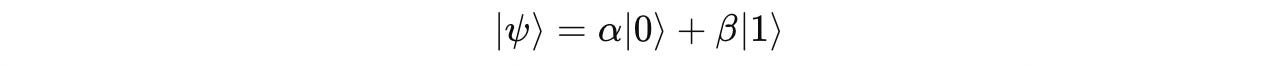
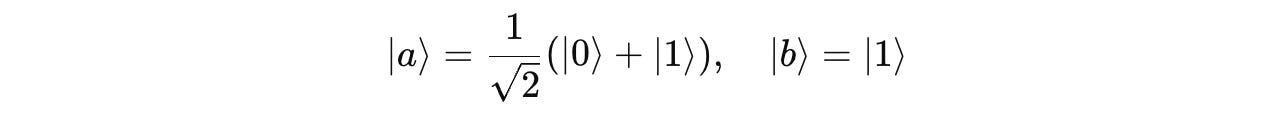
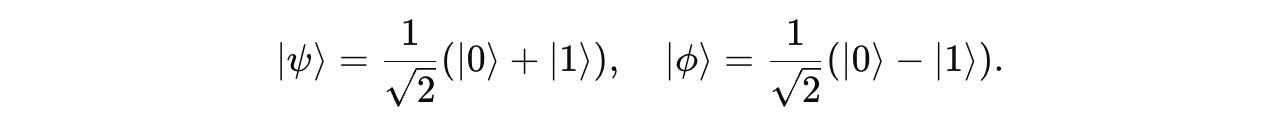
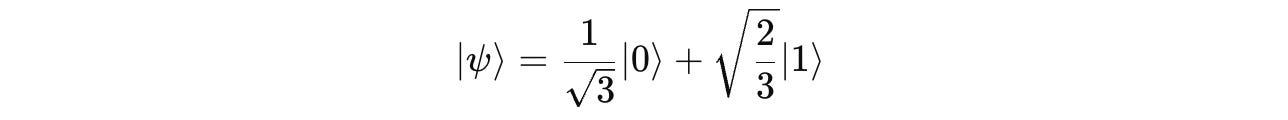
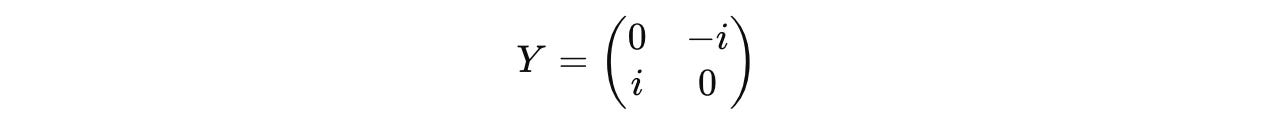
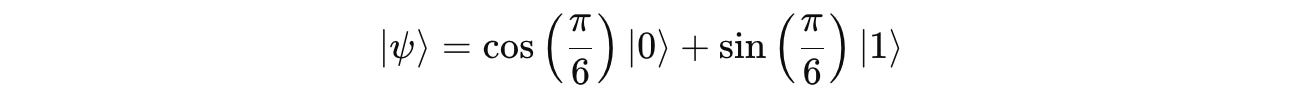

This is a realy solid set of questions for reinforcing the mathematical foundations. The progression from normalization through tensor products and inner products to eigenvalue decomposition makes sense pedagogically. Question 5 about the Pauli Y operator is particuarly useful since the imaginary unit in Y makes the eigenvector calculation less intuitive than X or Z. I'm curious about question 6 becuase measuring in the Hadamard basis requires transforming the computational basis state first. Are you planning to cover how these mathematical operations map to actual quantum circuit implementations in future posts?