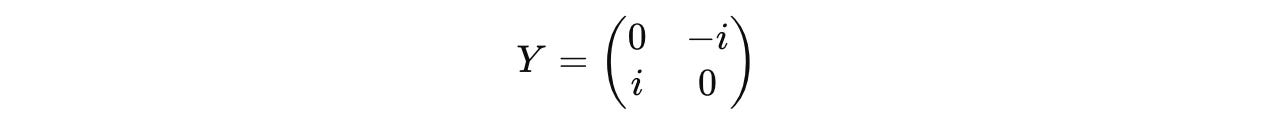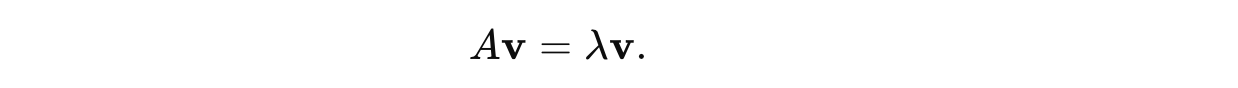Photograph of Satyendra Nath Bose, a theoretical physicist known for his work on quantum mechanics, which laid the foundation for Bose-Einstein statistics and the Bose-Einstein condensate theory. (Source)
In my previous post, I challenged you with six questions to help you strengthen the mathematical concepts that you need to master Quantum computing.
Let’s discuss the 5th question and solve it step by step using everything we have learned previously.
The question goes like this:
The Pauli-Y operator is defined as:
Find its eigenvalues and corresponding normalized eigenvectors.
Let’s solve this step by step.
What Are Eigenvectors?
Given a square matrix A of size n x n, an Eigenvector is a non-zero vector v that, when multiplied by A, results in a scalar multiple of itself.
Eigenvectors multiplied by A just scales (stretches or compresses) them without rotation or change in direction.
Check out the following equation. The scalar λin this equation is called the Eigenvalue.
Eigenvalue λ represents how much the eigenvector v is scaled (stretched or shrunk) by the transformation defined by the matrix A.
where:
A is the square matrix
v is the eigenvector of the matrix A
λ is the eigenvalue of the matrix A
In quantum mechanics, the square matrix A can represent Operators.
Operators are mathematical transformations that act on a quantum state to produce another quantum state.
If you’re looking for a detailed introduction to Eigenvectors, Eigenvalues, and Operators, the following lesson will help.
