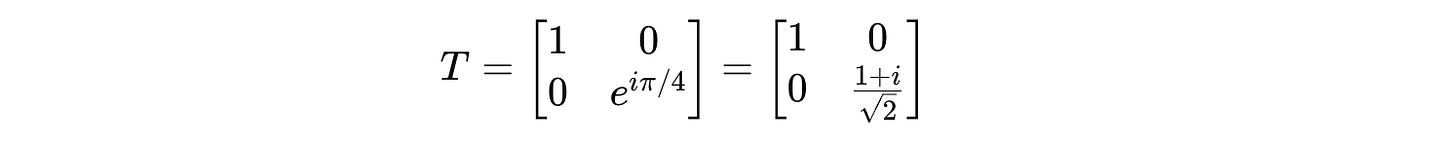Weekly Challenge: 5 Exercises For The Quantum Mind
Can you solve these 5 questions well by hand?
The aim of this publication has always been to teach Quantum Computing from the very basic mathematics in an easy to understand way.
If you’ve been following each week’s lesson in the publication from the beginning, you must have learned a good amount of Quantum Computing by now.
Let's get back to basics this week.
Before we dive into multi-qubit quantum gates, advanced quantum circuits, and quantum algorithms in future lessons, we need to make sure our foundations are rock solid.
So instead of another lesson, I'm giving you a challenge.
I want you to work through five problems completely by hand. No calculators, no AI assistance.
Think of this as your quantum fundamentals workout.
Ready? Here are the problems.
Problem 1
The Pauli-X gate acts as a quantum NOT gate and functions to flip a qubit state.
The following matrix represents it:
Apply this gate to a qubit in state |0⟩ and a qubit in state |1⟩.
What will the resulting states be after the application?
Problem 2
The Hadamard gate is used to create an equal quantum superposition state.
The following matrix represents it:
Apply this gate to a qubit in state |0⟩ and a qubit in state |1⟩.
What will the resulting superposition states be after the application?
Problem 3
Given the Pauli-X and Hadamard gates, compute the composite operation H(X(|1>)) and find the resulting matrix.
Problem 4
The T gate introduces a 45° phase difference between |0⟩ and |1>, which corresponds to a rotation of π/4 radians around the Z-axis of the Bloch sphere.
The following matrix represents it:
What power of the T gate is:
equal to the Z gate?
equal to the I gate?
Problem 5
You have previously learned about Rotation gates, which are single-qubit quantum gates that change a qubit’s state by performing rotations around specific axes of the Bloch sphere.
The following matrix represents it:
Apply the R(y)(π/3) gate to the following qubit, and calculate the initial and resulting probabilities of obtaining |0> and |1> when measuring the qubit.
Take your time working through these problems.
I'll post my detailed solutions by the end of this week so you can compare your approach with mine.
Don't worry if you get stuck. That's a completely normal part of the learning process, and I’m always approachable on the publication chat if you do.
See you soon!