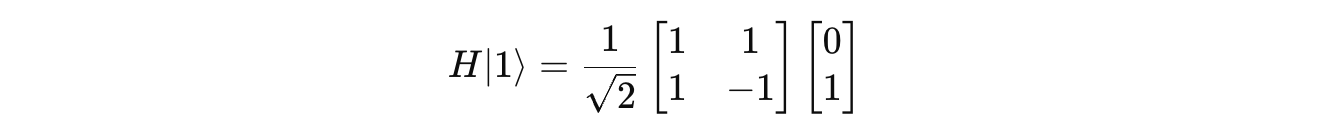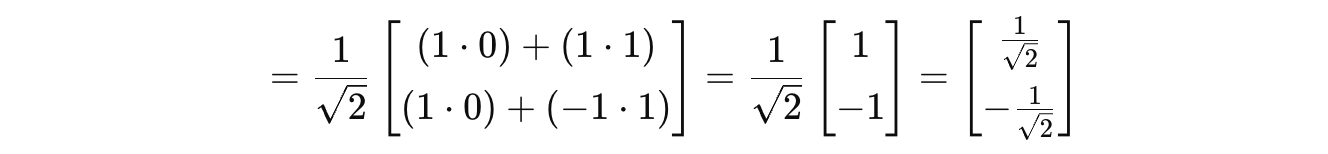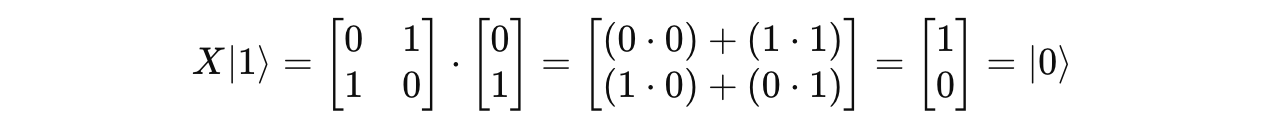Solution To Weekly Challenge: Problems 2 & 3
It's time to test your solutions!
Last week, I challenged you to solve five problems to help you revisit the fundamental mathematics of quantum computing.
We have already discussed the solution to the first problem.
Here are the solutions to the next two.
Problem 2
The Hadamard gate is used to create an equal quantum superposition state.
The following matrix represents it:
Apply this gate to a qubit in state |0⟩ and a qubit in state |1⟩.
What will the resulting superposition states be after the application?
Solution 2
Given the Hadamard gate H as represented by the following matrix:
We need to apply it to |0> and |1> which are represented by the following vectors:
Let’s first apply the H gate to |0> :
The final result is:
Next, let’s apply the H gate to |1> :
The final result is:
We confirm that the Hadamard gate puts a qubit into an equal probability superposition of |0> and |1>.
Problem 3
Given the Pauli-X and Hadamard gates, compute the composite operationH(X(|1>)) and find the resulting matrix.
Solution 3
We know that the following matrix represents the Pauli-X gate:
And the following matrix represents the Hadamard gate:
To calculate H(X(|1>)), we first calculate X(|1>) as follows:
Next, we apply the H gate to this result:
The final result is:
Message me or mention in the comments below if any of these steps are unclear.
See you in the next post with the solutions to Problems 4 & 5!