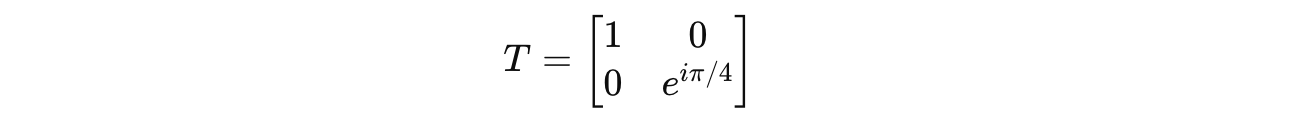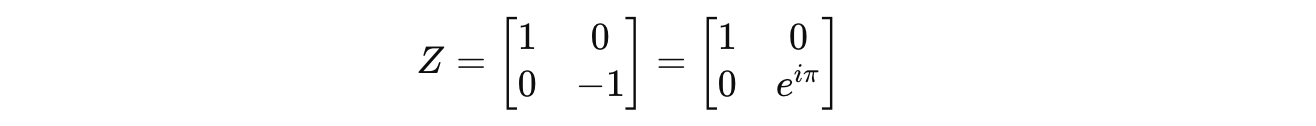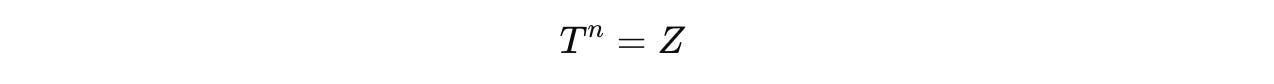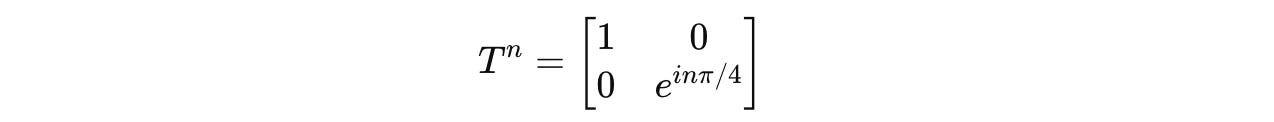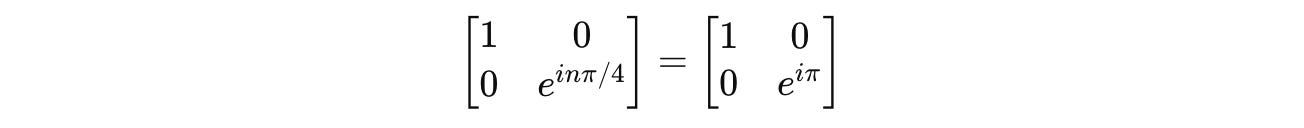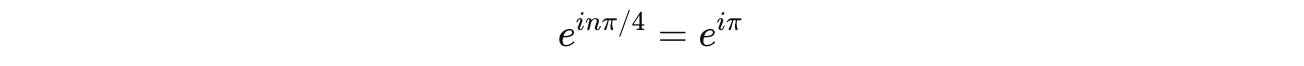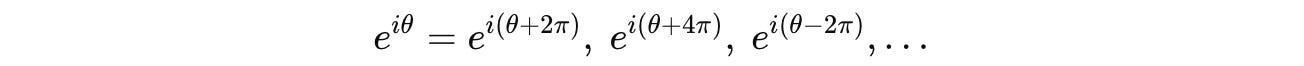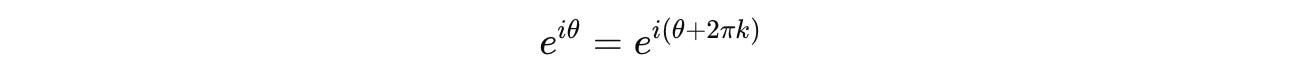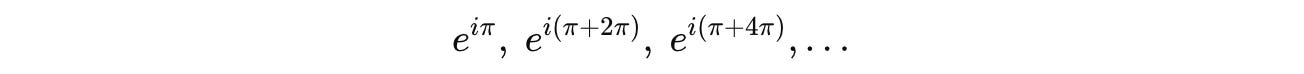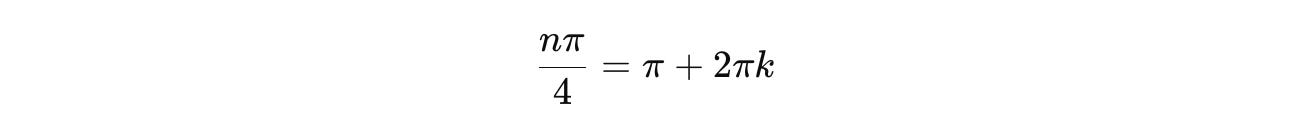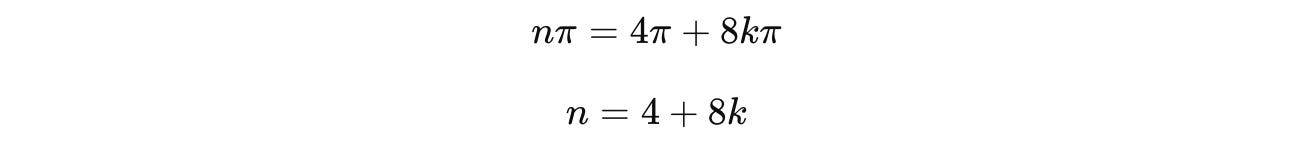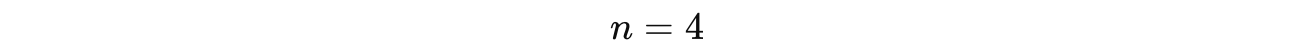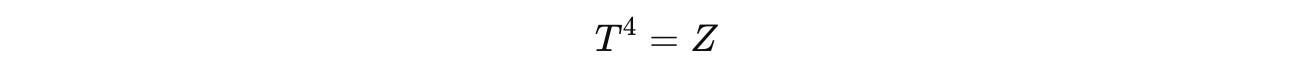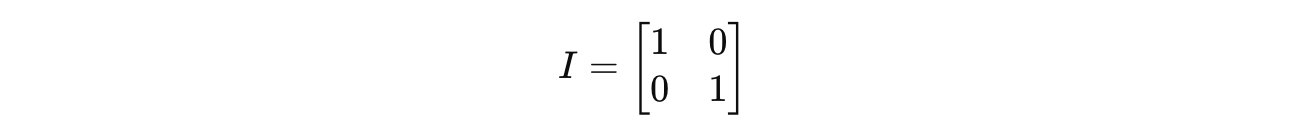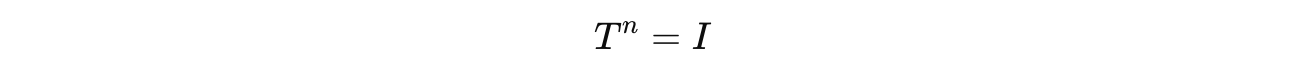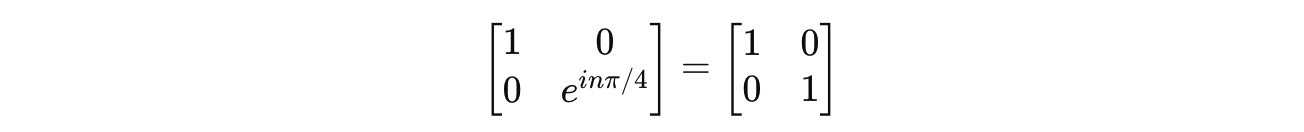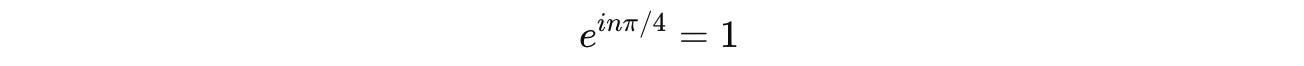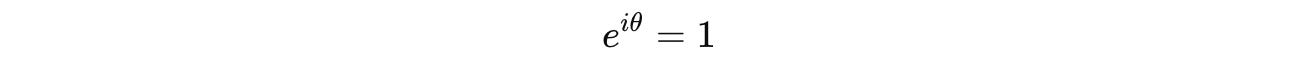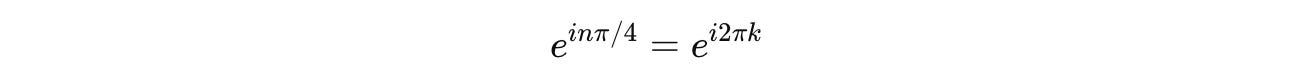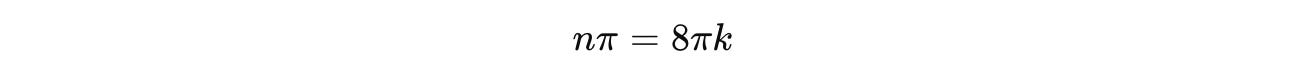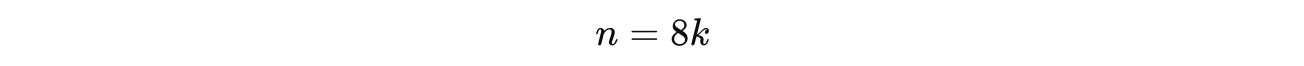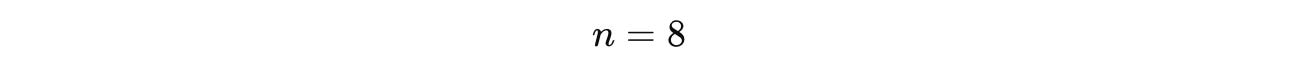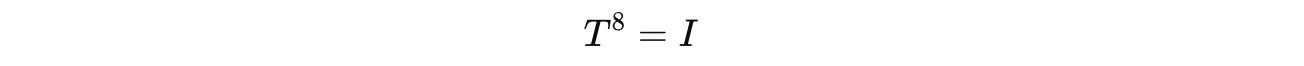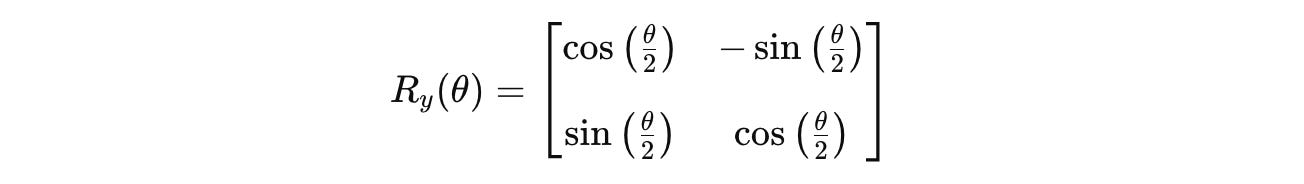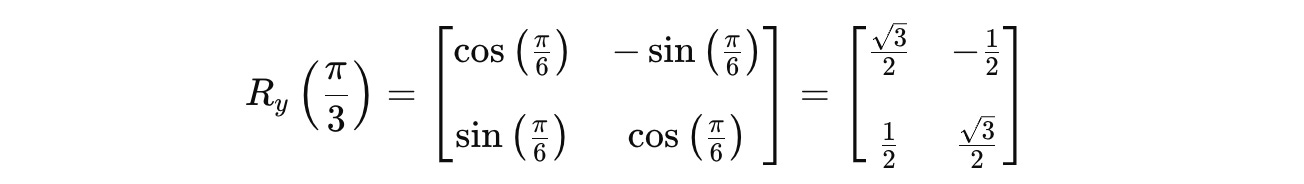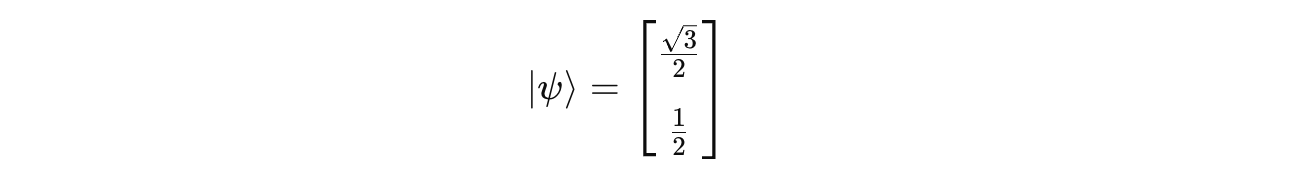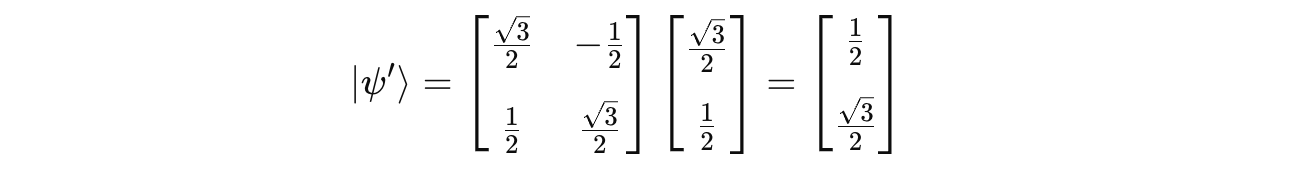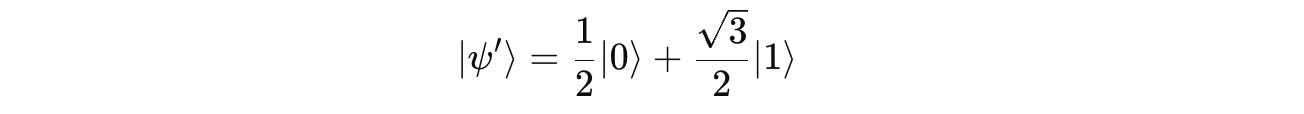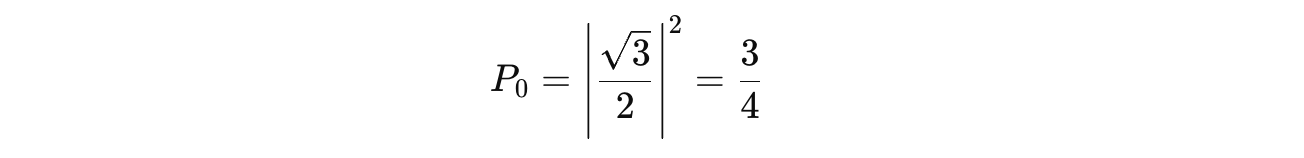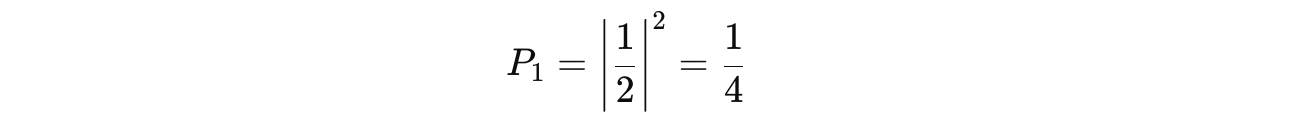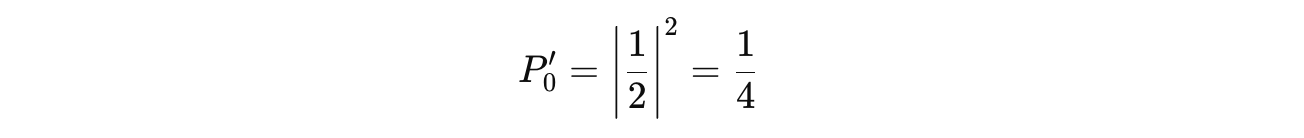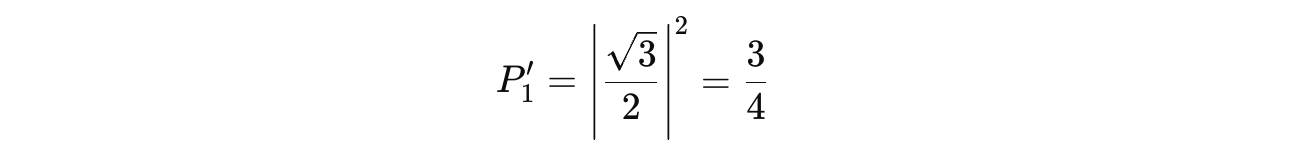Solution To Weekly Challenge: Problems 4 & 5

The final two solutions are here!

Paul Dirac and Richard Feynman at Jabłonna, Poland. July 1962. (Source)

In the last weeks, I challenged you to solve five problems to help you revisit the fundamental mathematics of quantum computing.

Weekly Challenge: 5 Exercises For The Quantum Mind

We have already discussed the solution to the previous three problems.

Here are the solutions to the last two.

---

Problem 4

The T gate introduces a 45° phase difference between |0⟩ and |1>, which corresponds to a rotation of π/4​ radians around the Z-axis of the Bloch sphere.

What power of the T gate is:

• equal to the Z gate?

• equal to the I gate?
  

Solution 4

The T gate is represented by the following matrix:

Let’s solve the first part of the problem: What power of the T gate equals the Z gate?

We know that the Z gate is represented by the following matrix:

(The above equation uses Euler’s Identity.)

What we need to find out is:

T^n can be written as:

When we equate it to the Z-gate:

We know that complex exponentials are periodic with a period of 2π, or:

Given:

We know that e^(iπ) is not unique, and it could also be:

Therefore, we write it as e^(π + 2πk), where k is an integer:

The smallest positive integer solution to this equation is:

Therefore:

---

Next, we will solve the second part of the problem: What power of the T gate equals the I gate?

We know that the Identity gate, or the I gate, is represented as follows:

We want to find out:

T^n can be written as:

When we equate it to the I-gate:

Using Euler’s Identity:

when θ = 2πk, where k is an integer.

The smaller positive solution to the equation is:

Which means that:

---

Problem 5

Apply the R(y)(π/3) gate to the following qubit, and calculate the initial and resulting probabilities of obtaining |0> and |1> when measuring the qubit.

Solution 5

We know that the general form of the R(y) gate is as follows:

For θ = π/3:

Given the qubit:

It can be written as a ket vector as follows:

Applying the rotation gate to this qubit results in:

The measurement probabilities of the qubit before applying the gate as shown below:

are:

• The probability of measuring |0>

• The probability of measuring |1>

The measurement probabilities of the qubit after applying the gate as shown below:

are:

• The probability of measuring |0>

  

• The probability of measuring |1>

---

I'm sure you would have learned a lot if you solved all five problems by hand.

If you did not, try going back to the challenge and working through the solutions step by step.

See you soon in the next lesson!