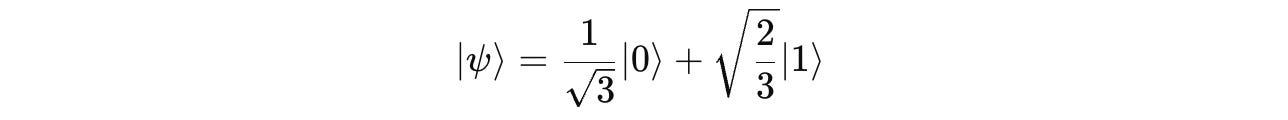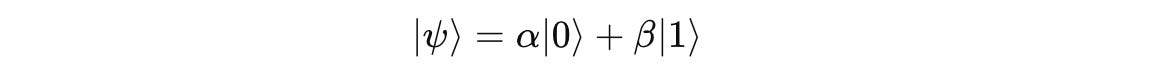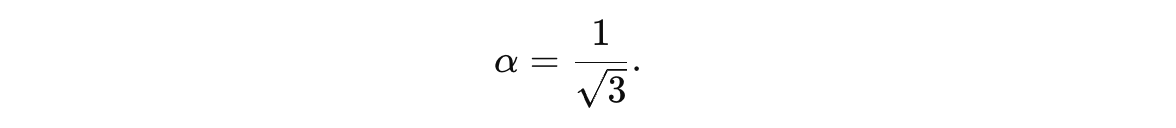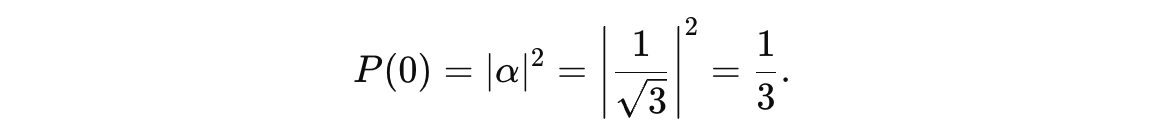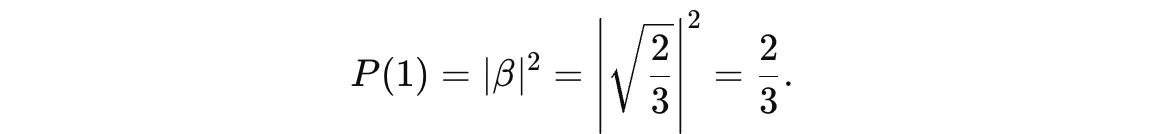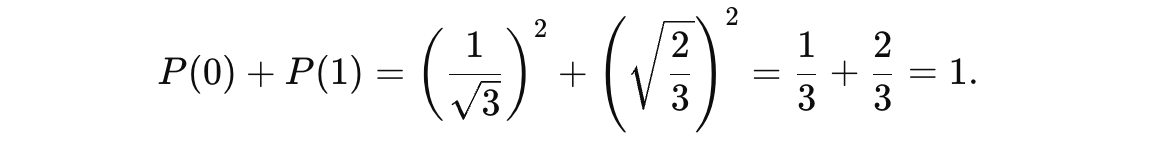How to Compute the Outcome Probabilities of Quantum Measurements

Solution to Question 4 of the ongoing quantum challenge.

Source: IBM

In my previous post, I challenged you with six questions to help you strengthen the mathematical concepts that you need to master Quantum computing.

Let’s discuss the 4th question and solve it step by step using everything we have learned previously.

The question goes like this:

Given a qubit in the following state:

If this qubit is measured in the computational basis, what is the probability of observing |0>?

This one is an easy one to solve. Let’s work on it!

---

On the computational basis {|0>, |1>}, a qubit is expressed in the form as follows:

For our given qubit, when expressed in this form, the probability amplitude of |0> is:

The probability of observing the state |0> is the squared magnitude of this amplitude α.

This is called Born’s rule.

Similarly, the probability of observing the state |1> is the squared magnitude of the amplitude β.

Both of these probabilities sum to 1, indicating that the quantum state is normalized correctly.

---

This is a short but very important calculation in Quantum computing, which you must know about.

See you soon in the next lesson!

Consider becoming a paid subscriber to ‘Into Quantum’ to master Quantum Computing from the ground up.