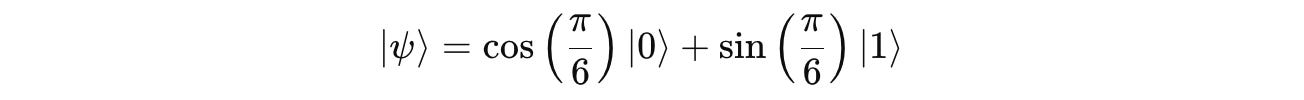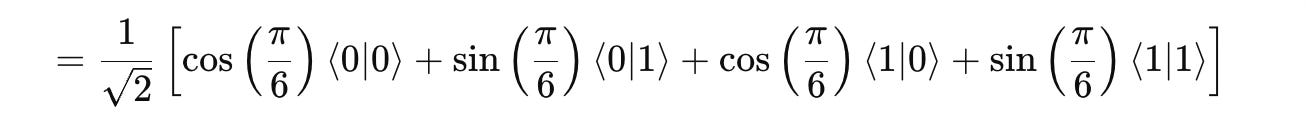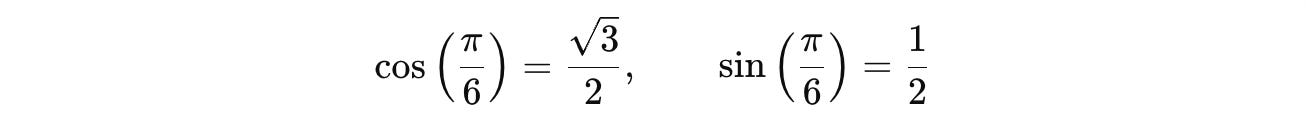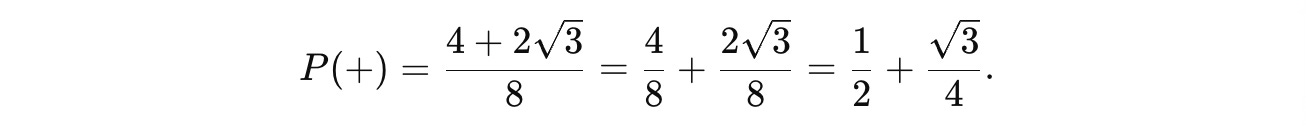How to Measure a Qubit in the Hadamard Basis
Solution to Question 6 of the ongoing quantum challenge.

In my previous post, I challenged you with six questions to help you strengthen the mathematical concepts that you need to master Quantum computing.
Let’s discuss the 6th and last question and solve it step by step using everything we have learned previously.
The question goes like this:
Given a qubit in the following state:
If we measure it in the Hadamard basis, what is the probability of obtaining |+>?
Here goes the solution.
We are given the following qubit:
We are asked to measure it in the Hadamard basis {|+>, |−>} which has the following basis states:
Then, we have to find the probability of obtaining |+>.
When we measure a quantum state |ψ> in a basis state |b>, we determine how much of |b> is contained in |ψ>. This is done by projecting |ψ> onto |b>.
The projection amplitude is calculated as <b | ψ>, and the probability of obtaining the outcome associated with |b> is:
In our case, this is:
Let’s first calculate <+| ψ>.
The state |+>:
In its bra form, it is written as:
From here:
Based on the orthonormality of basis states in the computational basis:
<0|0> = 1
<1|1> = 1
<0|1> = 0
<1|0> = 0
Using these values:
Given that:
This leads to:
This is the probability amplitude for obtaining the outcome |+> when measuring the given qubit.
Next, the probability of obtaining the outcome |+> when measuring the given qubit is:
This is approximately 93.3%, and this is our answer.
That’s everything for this article.
Thanks for being a curious reader of Into Quantum, a publication that teaches essential concepts in Quantum Computing from the ground up.
To get even more value from this publication, consider becoming a paid subscriber.
See you soon in the next lesson.