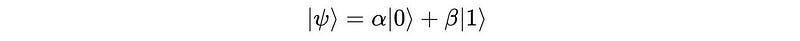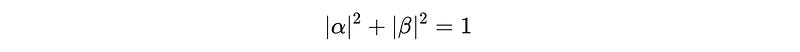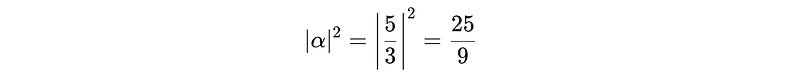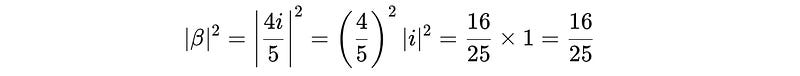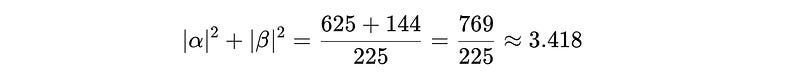How To Check Whether A Qubit State Is Normalized?

Solution to question 1 of this week's quantum challenge.

Photograph of Albert Einstein’s desk taken a few hours after he died. Princeton, New Jersey, April 1955. (Source)

In the last post, I challenged you with six questions to help you strengthen the mathematical concepts that you need to master Quantum computing.

Let’s go to the first question and solve it step by step using everything that we have learned previously.

The question goes like this:

A single qubit is in the state:

where α = 5/3​ and β = 4(i)/ 5.

Verify if this is a valid quantum state by showing that it is normalized.

---

Why Normalization?

We know from the previous lessons that the following equation represents a single qubit’s state:

where α and β are complex probability amplitudes.

The squares of these amplitudes represent the probability of obtaining either |0⟩ or |1⟩ when the qubit is measured.

Normalization means that the total probability of all possible outcomes of a qubit’s state (|0⟩ or |1⟩ in this case) equals 1.

A qubit’s state must be normalized for it to be valid and make sense.

(You don’t want them to sum to 0.6, and then wonder why there’s a void of the rest of the 0.4? The world doesn’t work like that.)

---

Checking For Normalization

Given the qubit has the probability amplitudes as α = 5/3​ and β = 4(i)/ 5.

The square of the first probability amplitude is:

This is the probability of obtaining |0> when the qubit is measured.

The square of the second probability amplitude is:

Adding them up results in:

This is not equal to 1.

This means the qubit isn’t normalized and isn’t a valid state.

---

I hope that you were able to solve this question by hand. See you soon in the next lesson!

Consider becoming a paid subscriber to ‘Into Quantum’ to master Quantum Computing from the ground up.