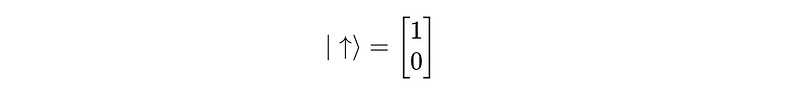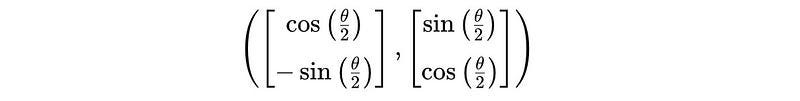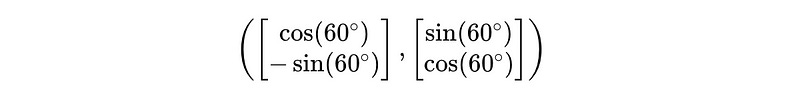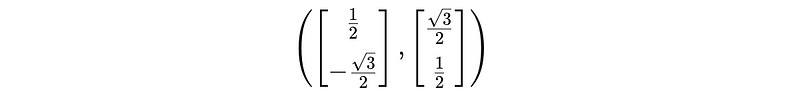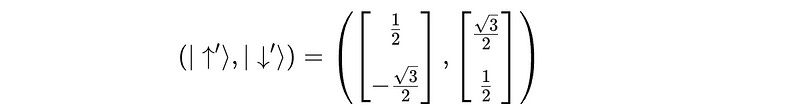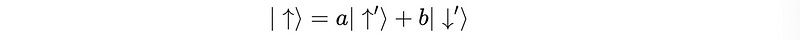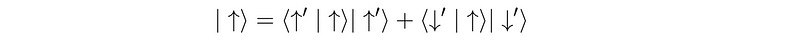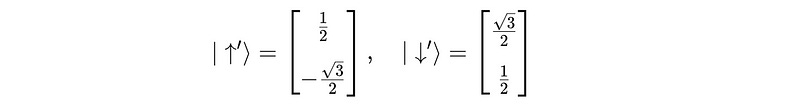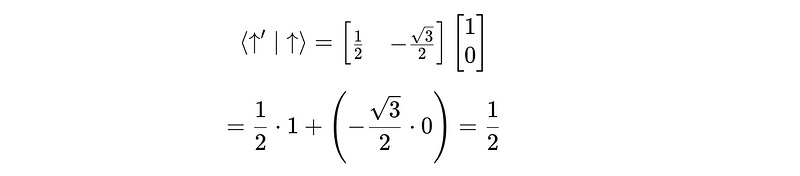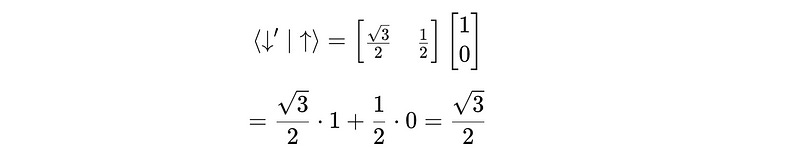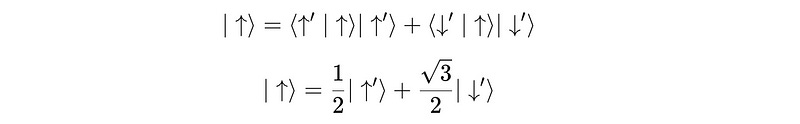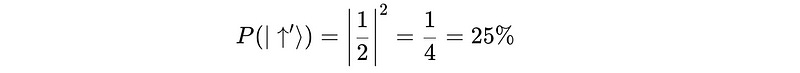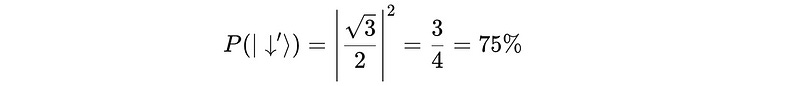Combining Our Learnings So Far: Basis Rotation & Probability Amplitude Calculations

Let's step by step solve a problem to solidify our understanding of Quantum calculations

Photograph of Ocelot, the first-generation quantum chip developed by the AWS Center for Quantum Computing that promises to reduce quantum error correction by up to 90% and accelerate the development of real-world quantum computing applications (Source: AWS; The Wall Street Journal)

Here’s a problem statement:

Given a spin-up electron (qubit) in the standard basis (0° orientation), we need to measure it using a measuring apparatus rotated by 120° and find the probability of obtaining spin-up in the new rotated basis.

Let’s solve it using what we learned from the last lesson.

We are given a spin-up electron (qubit) in the standard basis:

When the measurement apparatus is rotated by 120°, the following transformation matrix gives the associated basis for the rotated system — 

Substituting the values with θ/2 = 120°/2 = 60° , we get:

These values represent the new measurement basis when the apparatus is rotated by 120°.

To make it more clear:

• The first ket vector/ column is the new “spin-up” state in the rotated basis

• The second ket vector/ column is in the new “spin-down” state on a rotated basis.

---

Btw, my book “Computer Science In 100 Images” is currently available at a 40% discount for early readers. Grab your copy using this link.

---

Moving on to the next part of the problem statement:

Find the probability of obtaining spin-up in the new rotated basis.

We start by expressing ∣↑⟩ as a linear combination of the new basis vectors.

The probability amplitudes a and b can be further expanded to the following:

(Remember, this is similar to what we did in the previous lesson.)

Let’s now calculate them using the following results:

To find a, we calculate the inner product ⟨↑′∣↑⟩:

Similarly, to find b, we calculate the inner product ⟨↓′∣↑⟩:

(If this calculation confuses you, this lesson will help you revisit the basics.)

Let’s substitute the above-obtained values in the equation:

We know that the square of the respective probability amplitudes gives the probabilities of obtaining each state.

Therefore, the solution to our problem of the probability of measuring ∣↑′⟩ (new spin-up) is:

And the probability of measuring ∣↓′⟩ (new spin down) is:

---

I hope that these calculations make sense. See you soon for another exciting and fundamental lesson on Quantum computing!

Thanks for being a curious reader of “Into Quantum”, a publication that aims to teach Quantum Computing from the very ground up.