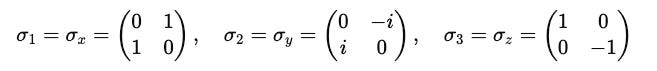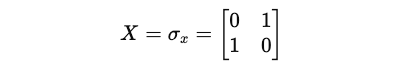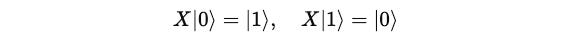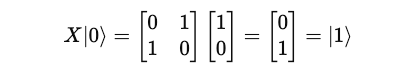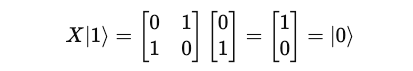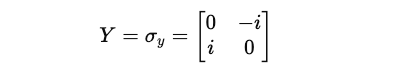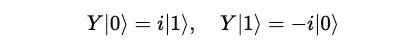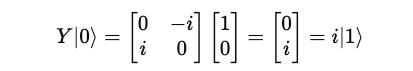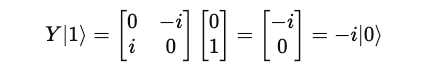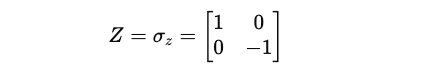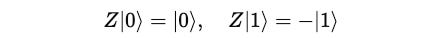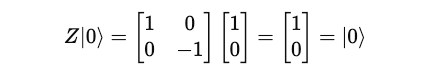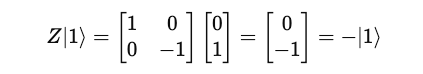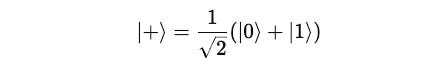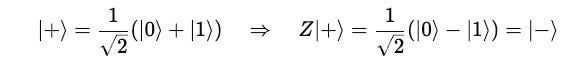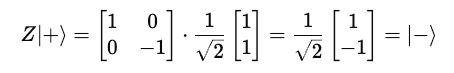A Lesson On Pauli Matrices As Quantum Gates

Learn about Pauli-X, Y & Z gates in depth and visualise their operations on the Bloch sphere.

A photograph of Wolfgang Pauli, a pioneering physicist best known for the Pauli Exclusion Principle, which revolutionized quantum mechanics and earned him the 1945 Nobel Prize in Physics. (Source)

In the last lesson, we learned about the mathematics behind Pauli matrices.

We learned that they are Unitary, which makes them suitable for use as quantum gates. This is a lesson where we understand how.

---

What Are Pauli Matrices?

The Pauli matrices are a set of three 2 x 2 complex matrices that are fundamental to quantum mechanics.

These are:

• Pauli-X (σ(x) or σ(1))

• Pauli-Y (σ(y) or σ(2)), and

• Pauli-Z (σ(z) or σ(3))

They are named after the phenomenal physicist Wolfgang Pauli, who won the 1945 Nobel Prize in Physics for discovering the Pauli exclusion principle.

---

Pauli Matrices As Quantum Logic Gates

Pauli matrices act on a single qubit and change its state. Therefore, they are also called Single-qubit gates.

Pauli-X Gate/ X-Gate

The Pauli-X matrix (also called the X-gate) is shown below:

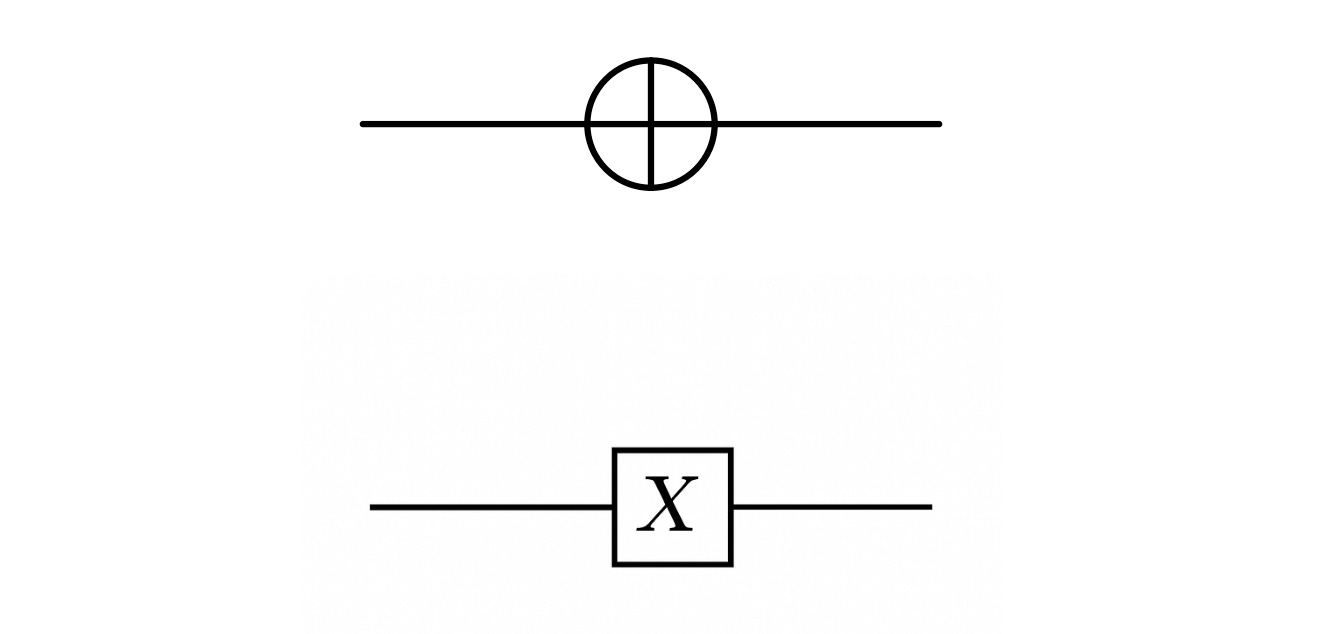
It is visually represented by either of the following symbols:

It is equivalent to the NOT gate in classical computing.

This gate swaps the amplitudes of |0⟩ and |1⟩ which is similar to the bit-flip operation of the classical NOT gate.

This means that when the gate acts on a qubit in state |0>, its state is flipped to |1> and vice versa.

This is how these results are obtained:

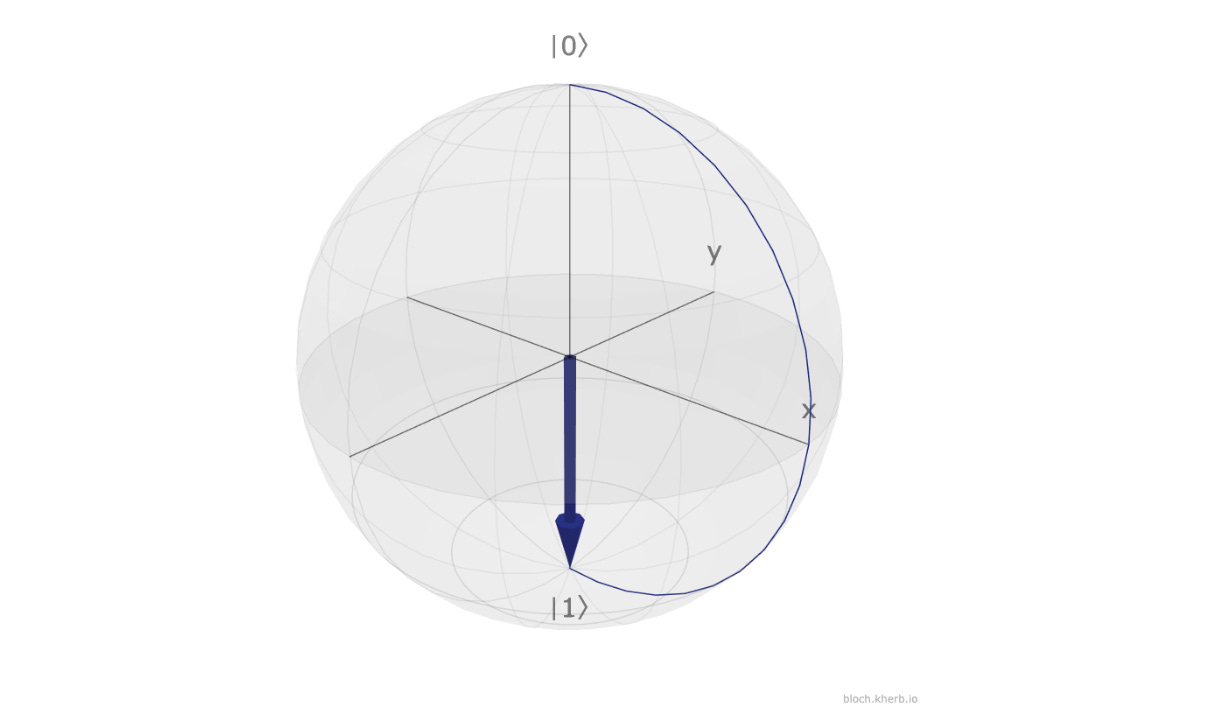
On the Bloch sphere, this is equivalent to rotating the qubit 180° around the X-axis.

Pauli-X gate applied to a qubit in state |0> rotates it by 180° around the X-axis (Source)

---

Pauli-Y Gate/ Y-Gate

The Pauli-Y matrix (also called the Y-gate) is shown below:

It is visually represented by the following symbol:

This gate leads to a combination of a bit flip and a phase flip for a qubit’s state.

Its operation on |0> and |1> are shown below:

This is how these results are obtained:

On the Bloch sphere, this is equivalent to rotating the qubit 180° around the Y-axis.

Pauli-Y gate applied to a qubit in state |0> rotates it by 180° around the Y-axis (Source)

---

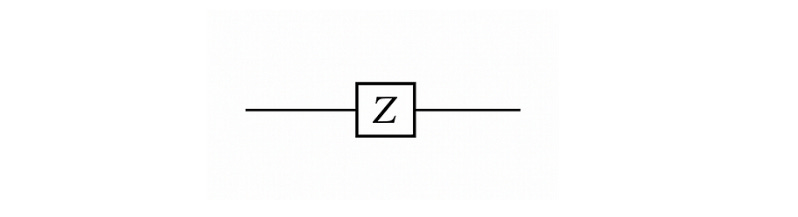
Pauli-Z Gate/ -Gate

The Pauli-Z matrix (also called the Z-gate) is shown below:

It is visually represented by the following symbol:

This gate causes a phase flip for a qubit in state |1> but leaves |0⟩ unchanged.

Its operation on |0> and |1> are shown below:

This is how these results are obtained:

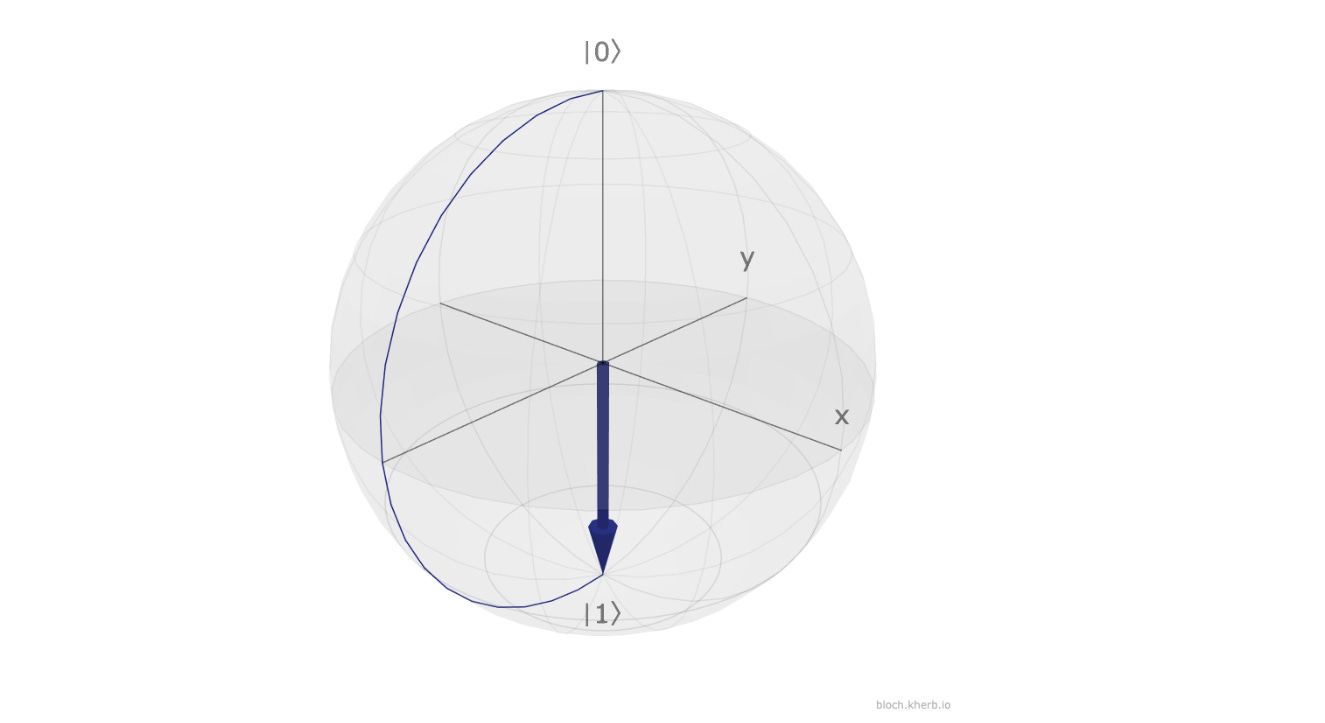
On the Bloch sphere, this is equivalent to rotating the qubit in state |1> by 180° around the Z-axis.

Note that for a qubit in state |1>, the position is not changed after the application of Z-gate.

This is because a change of global phase has no observable effect on the Bloch sphere. Only the relative phase is visualised on the Bloch sphere.

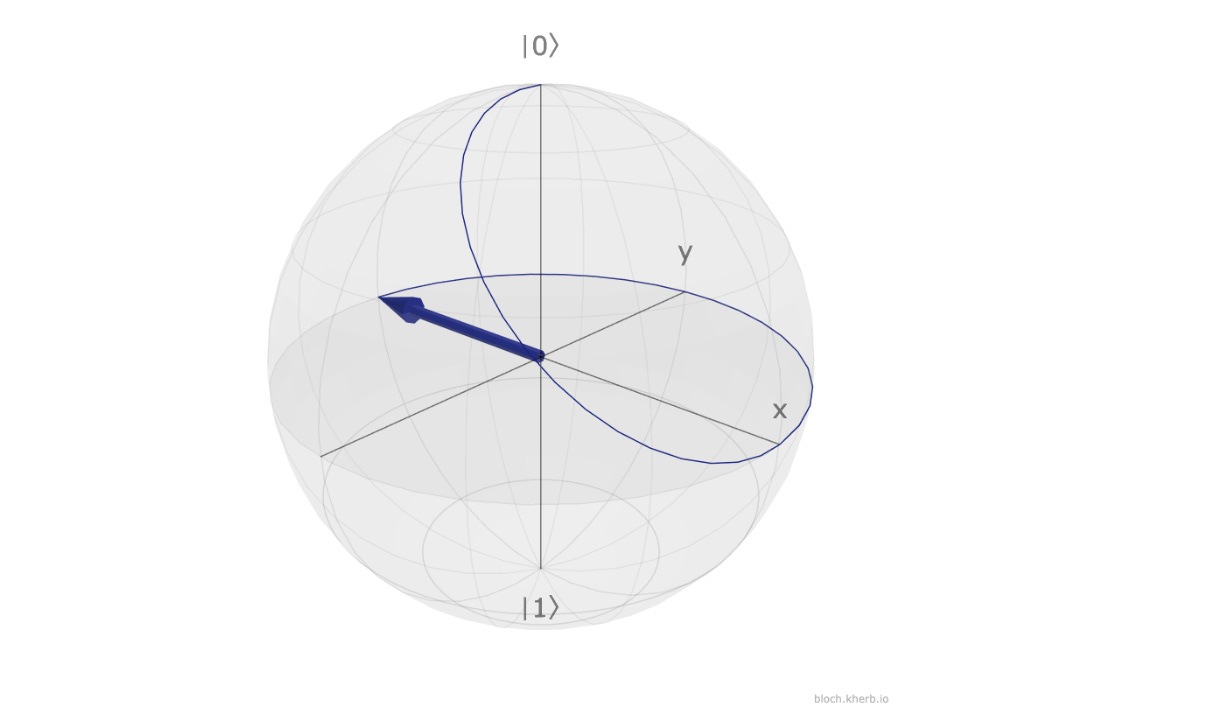
Take an example of applying the Z-gate on a qubit in an equal superposition state represented by |+>.

This state lies on the positive X-axis of the Bloch sphere.

Applying the Z-gate changes the relative phase between the components as shown below:

The resulting state represented by |-> lies on the negative X-axis of the Bloch sphere.

This is how these results are obtained:

The above operation causes the state to rotate on the Bloch sphere around the Z-axis as shown below:

Pauli Z applied to a qubit in state |+> (prepared by applying the Hadamard gate to qubit |0>) rotates it by rotates it by 180° around the Z-axis (Source)

---

That was all about Pauli matrices used as Quantum logic gates.

Thanks for being a curious reader of “Into Quantum”, a publication that aims to teach Quantum Computing from the very ground up.

See you soon in the next lesson!