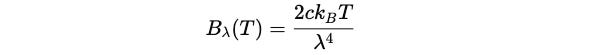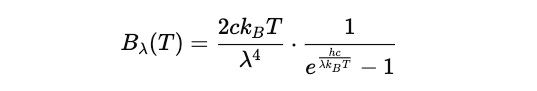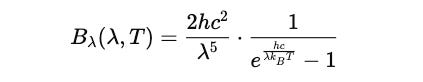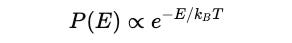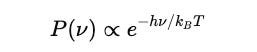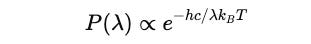The Story Of How 'Quantization' Changed Classical Physics Forever
Principle 3: Many fundamental physical properties can only exist in discrete values (Quanta) rather than a continuous range.

It is 1897.
The famous physicist William Thomson, Lord Kelvin, famously concludes:
“There is nothing new to be discovered in physics now. All that remains is more and more precise measurement.”
And if you were a physicist who lived in the late 19th century, you might have felt this way as well.
Isaac Newton’s laws of motion had stood the test of time for over 200 years. They could near-accurately describe planetary motion, falling objects, and the mechanics of everyday life.
James Clerk Maxwell’s equations unified electricity, magnetism, and light into a single framework.
Statistical mechanics had been developed and it explained how temperature, pressure, and entropy result from atomic motion.
Everyone felt that the precise measurements were the way forward to refining the existing theories rather than developing new theories that could overthrow the previous ones.
There were just a few unsolved problems on the way, and one of them was about to prove everything wrong.
The Flaw In Rayleigh-Jeans Law For Blackbody Radiation
Let’s learn what a black body is first.
It is an ideal object that absorbs all incoming light rather than reflecting it and perfectly emits radiation across all frequencies.
Because it absorbs all visible light, its surface appears black, which is why it is called a black body.
Physicists create an approximate black body using a hollow metallic sphere/ box with a small hole. Any light entering this hole gets reflected multiple times inside until fully absorbed.
Next, heating the black body to high temperatures causes it to emit radiation.
The spectral radiance (or specific intensity) of this radiation is described using the Rayleigh-Jeans Law:
where:
Bλ(T)is the spectral radiance per unit wavelength (power emitted per unit area, per unit solid angle, per unit wavelength)cis the speed of light in a vacuumk(B) is the Boltzmann’s constantTis the absolute temperature of the blackbodyλis the wavelength of the emitted radiation
In easy words, the formula gives the intensity of radiation emitted by a black body for a given wavelength (λ) and temperature (T).
Note that the intensity of radiation increases proportionally with temperature T but is inversely proportional to the fourth power of the wavelength λ⁴.
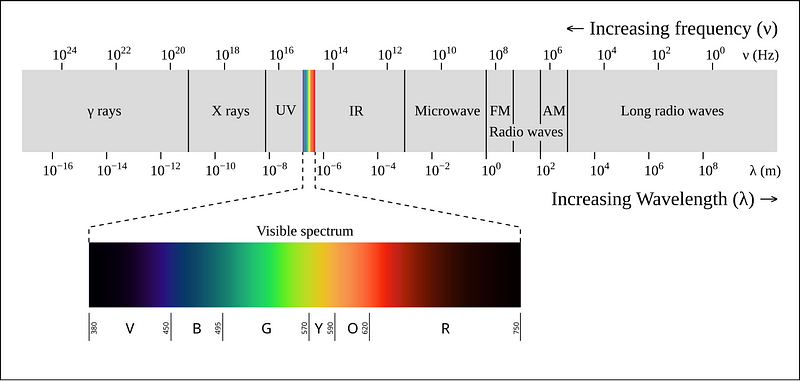
Look at the electromagnetic spectrum shown in the image below.
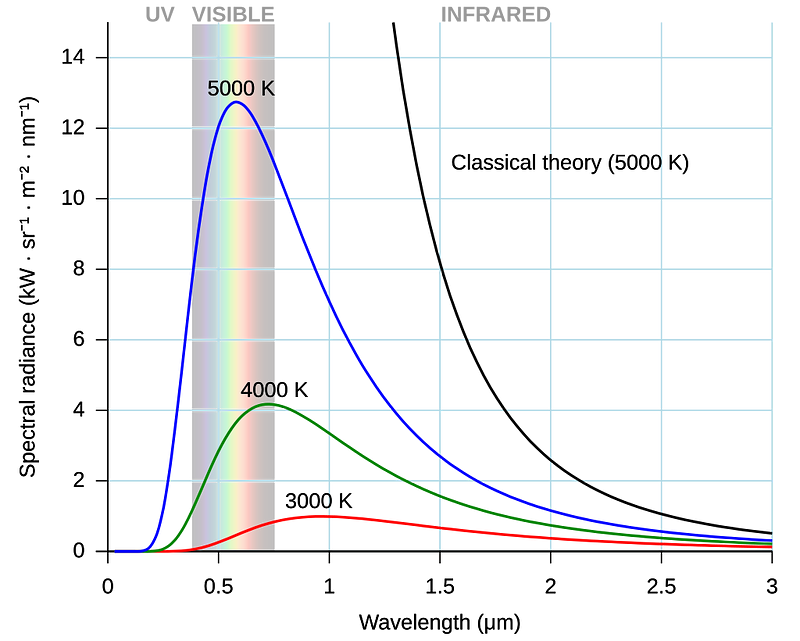
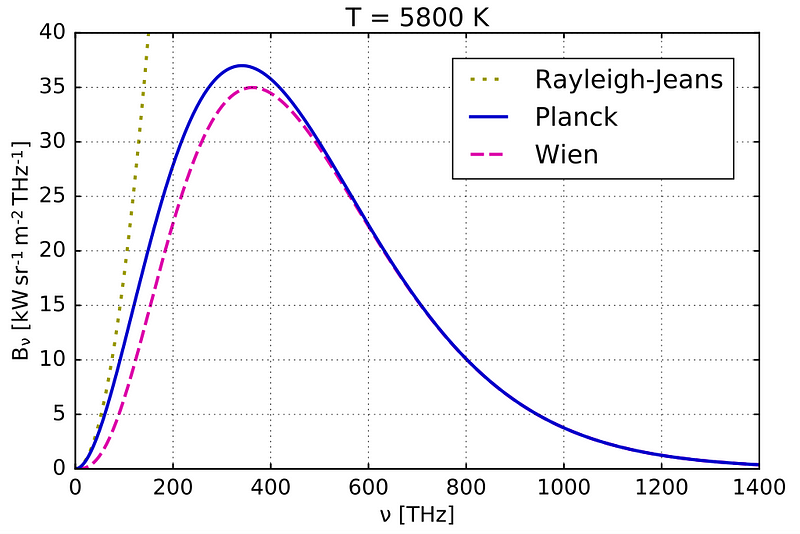
Rayleigh-Jeans law accurately predicts the spectral radiance at large wavelengths, but as we move towards the UV spectrum, it predicts infinitely increasing intensity.
This means that following the law, a black body must emit infinite energy at short wavelengths — which is physically impossible.
This shortcoming of the law is called “Ultraviolet Catastrophe”.
This was one of those unsolved problems that was bothering classical physicists for a long time.
Max Planck Enters The Game
Max Planck, startled by this problem, found a mathematical workaround for it.
He added an exponential suppression term to Rayleigh-Jeans law to fix its result at shorter wavelengths.
This can also be written as:
This was based on his wild assumption that electromagnetic radiation can be emitted or absorbed only in discrete packets, called Quanta of energy.
This was a bizarre idea for this time which was dominated by classical physics.
In classical physics, energy was assumed to be continuous, and the Rayleigh-Jeans Law assumed that energy could be divided into arbitrarily small amounts and was distributed equally across all frequencies.
Planck instead proposed that energy is quantized rather than continuous and could only be transferred in packets that were calculated using:
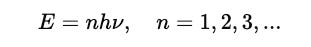
To modify the classical formula, he used Boltzmann’s statistical mechanics, which tells that the probability of a system having energy E at temperature T follows the given proportionality:
Since he assumed that energy is quantized as E = hν, the probability of a system emitting a radiation of frequency ν is:
With ν = c / λ :
This is where the exponential suppression term comes from.
His theory showed that for low-frequency photons (small hν), this exponent is close to 1, meaning radiation is easily emitted.
But for high-frequency photons (large hν), the exponent decreases exponentially, making emission extremely unlikely.
This led to the formulation of the Planck radiation law.
At first, even Planck believed in his own theory and thought that it was just a clever mathematical fix.
But experiments aligned perfectly with what he had described, with him being unaware that he was about to change the course of Physics forever.
Einstein Finally Solves It For Everyone
It was in 1905 that Albert Einstein took forward Planck’s theory and applied it to light.
This was while experimenting with the Photoelectric effect, where light hitting a metallic surface could lead to the knocking out of electrons and the production of electricity.
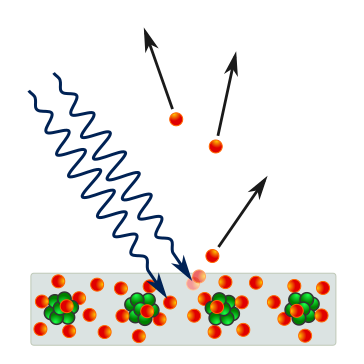
As per classical physics, light is a wave.
If this were true, increasing its intensity would have ejected more electrons, but it didn’t work that way.
Instead, Einstein proposed that light is made of quantized packets called photons and that the energy of each photon was given by E = hν.
It was only if the photon’s energy (based on its ν) was high enough that it could knock out an electron and that no amount/ intensity of low-energy photons could make this happen.
And, light had to be quantized to explain this experiment.
Planck’s contributions to Physics were recognized, winning him the 1918 Nobel Prize in Physics for his discovery of energy quanta and quantum theory.
Albert Einstein was later (in 1921) awarded the Nobel Prize in Physics for discovering the law of the photoelectric effect.
Since then, many physical properties (energy levels in atoms, charge, and angular momentum) have been proven to be quantized.
These were the early ideas and experiments that led to the development of Quantum Mechanics, which has now entirely replaced classical physics at atomic and subatomic scales.
Thanks to Planck, this is the theory that now makes Quantum computing possible.
Thanks for being a curious reader of “Into Quantum”, a publication that aims to teach Quantum Computing from the very ground up.
See you soon in the next lesson!