Linear Combinations Are The Secret Behind Quantum Mechanics
A lesson on Linear Algebra and why you should pay attention to it!
This week’s newsletter is written by Serena Krejci-Papa from Science with Serena.
She is an author who transforms complex topics in quantum science, physics & chemistry into compelling stories for all audiences.
She graduated from Case Western Reserve University with a B.S. in Chemistry and is currently pursuing my masters in Theoretical and Computational Chemistry in the Erasmus Mundus Joint Master Program in Barcelona.
Follow and connect with her through the links below:
Substack newsletter The Quantum Notebook
Let’s get started!
Wait!
Before you call me a nerd and click out of this article because I said linear algebra, hear me out.
Linear algebra is more than just a type of math; it’s the secret to the wonder and uniqueness of all the subjects you know and love, like quantum mechanics, machine learning, artificial intelligence, or computer science.
That’s right!
Linear algebra was the first person to be nice to these guys on freshman orientation day, and now they’re inseparable. So, if you want to get to know one, you’re going to have to get to know the other.
Relax. In the end, they’ll both be your friends.
Let’s get into it.
Why Linear Algebra?
Linear algebra is like algebra except we perform operations with lines and multi-dimensional spaces instead of 2D points on a grid.
It’s extremely cool and an extremely powerful mathematical lens we can use to make sense of the world when it doesn’t make sense.
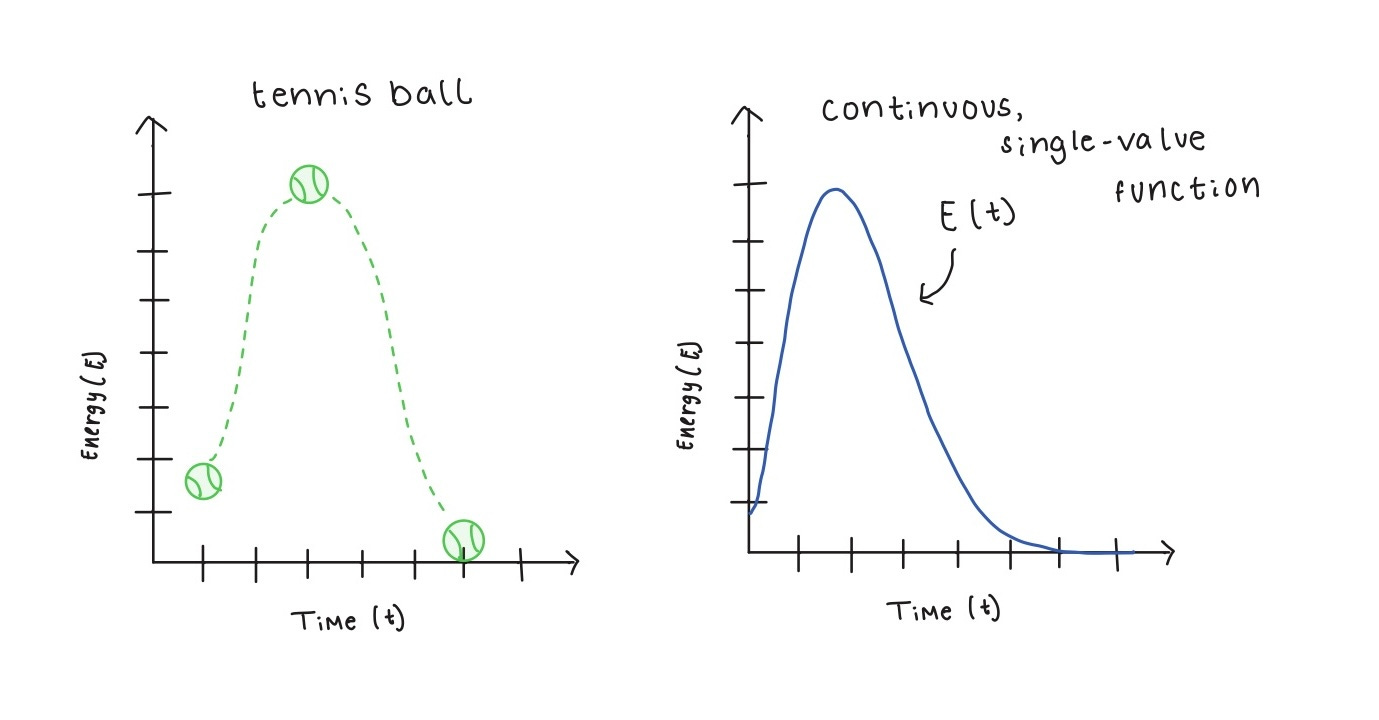
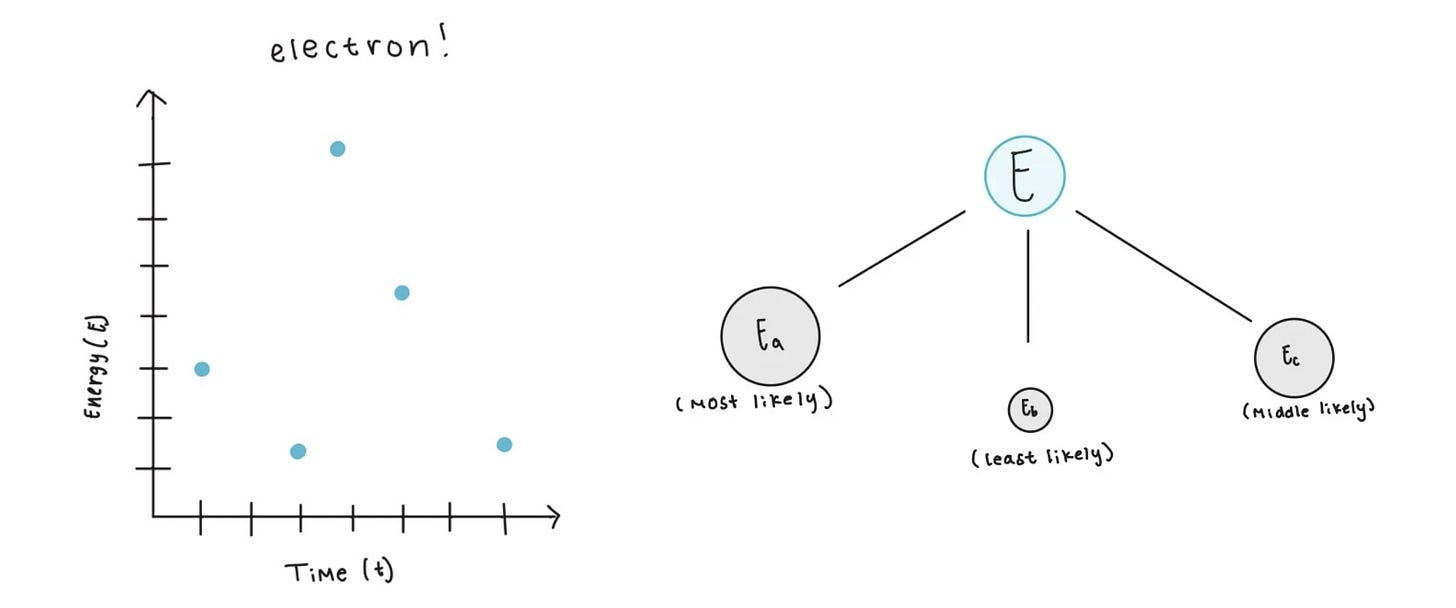
For example, it can explain why electrons don’t behave like tennis balls.
Tennis balls can be modelled with continuous, single-valued functions because they behave like continuous single-valued functions: they go up, make an arch, and then come back down.
They never disappear and reappear somewhere else, or exist in two places at once.
Since we can see this behavior with our eyes, it’s only natural to presume that the entire world works like this, with continuous, single-valued functions.
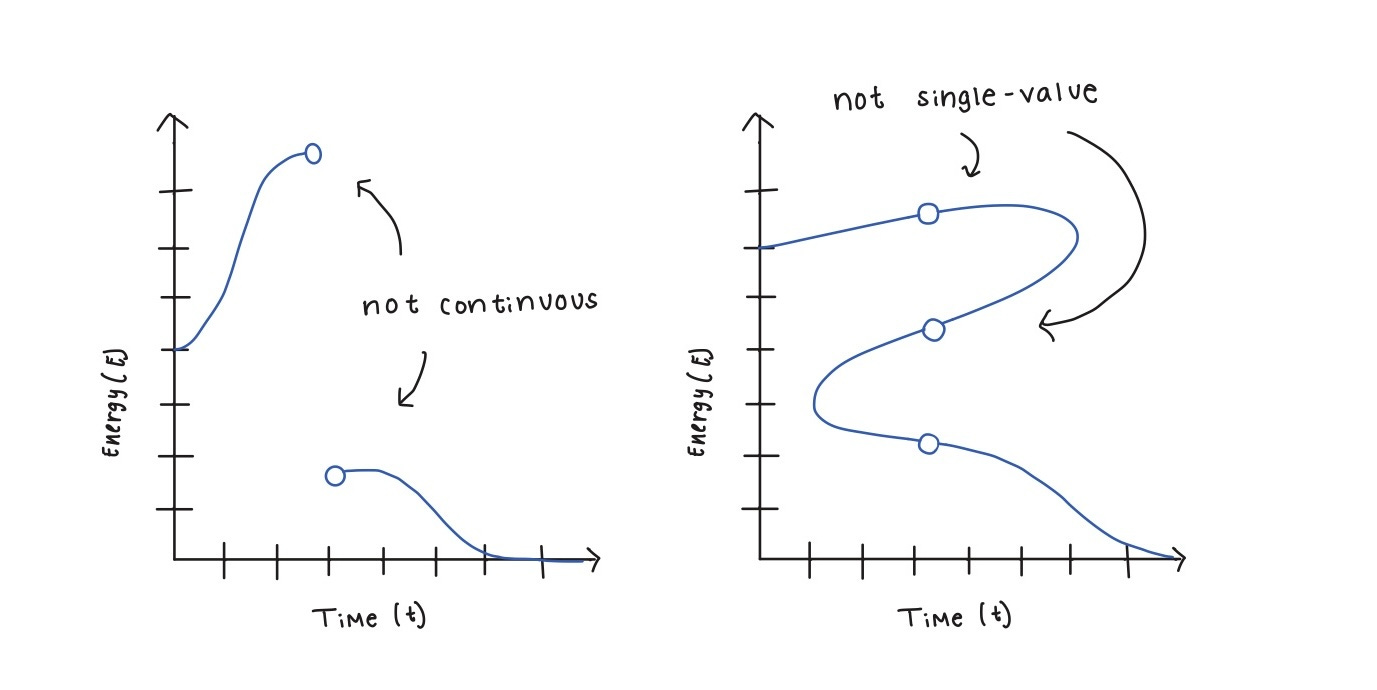
Electrons don’t follow this rule.
They don’t release energy continuously like a tennis ball, but release energy in discrete values at specific but random intervals that are different every time. There is some rhyme and reason to it, but only the fact that some discrete energy values are more likely than others.
What function can describe this?
Functions — hell no, but linear algebra — hell yes!
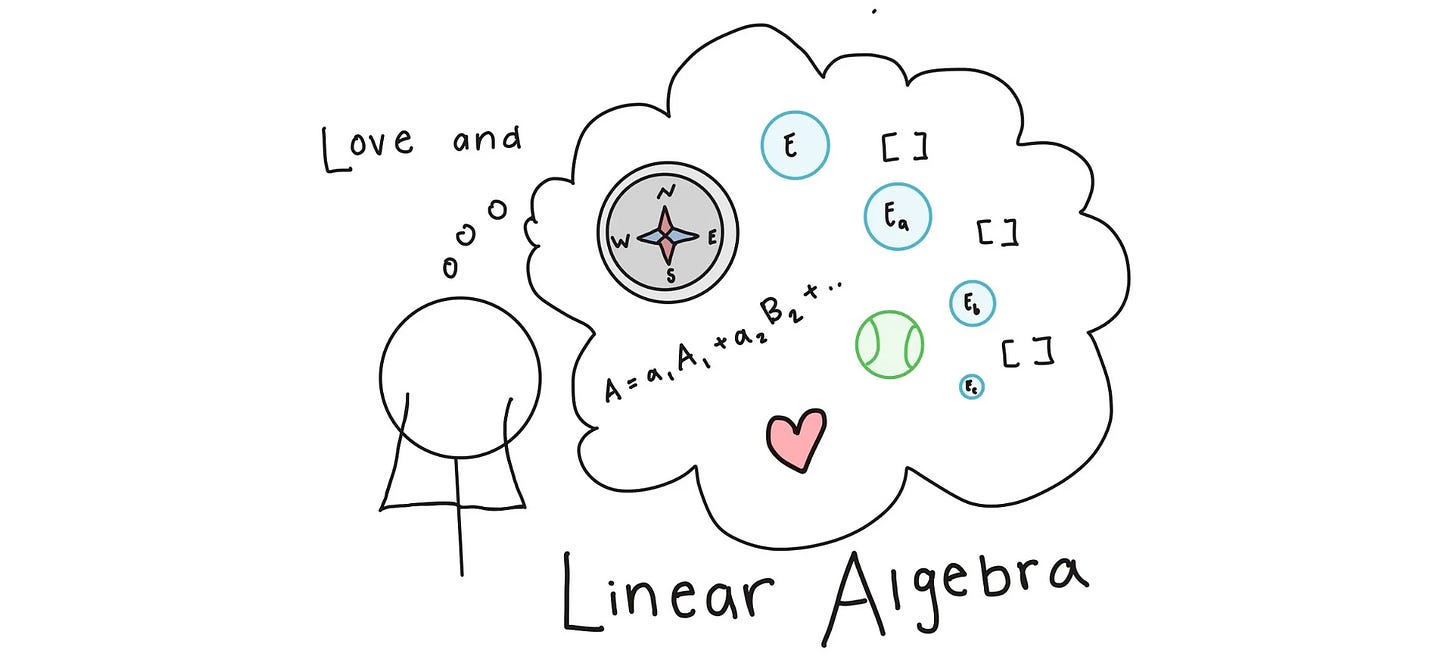
Linear Combinations
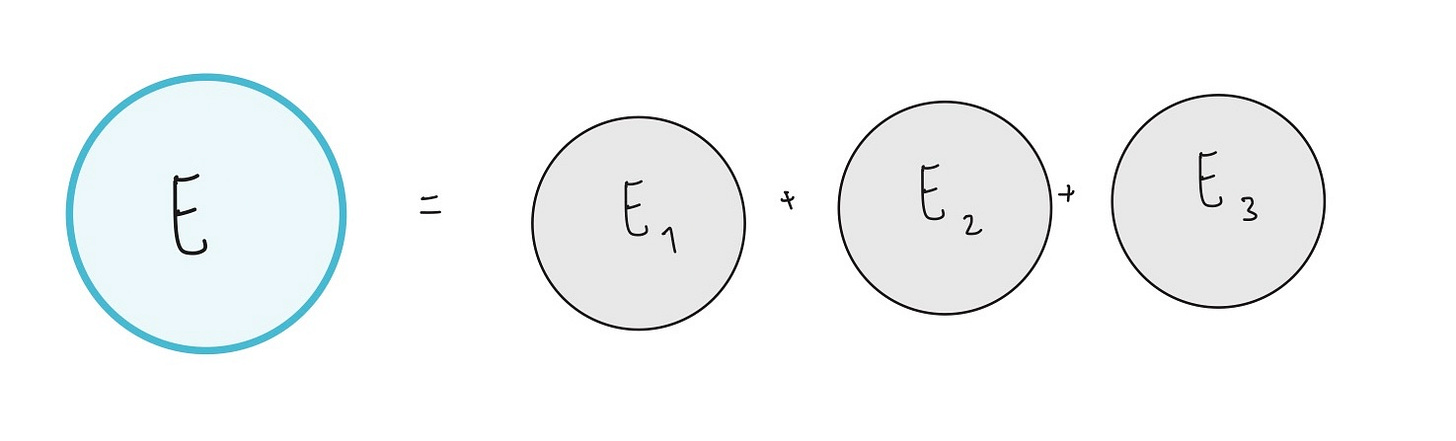
Linear combinations are a concept in linear algebra and the perfect mathematical tool to represent an electron.
They can represent one state as a combination of many, which is exactly what we need. Here’s what it looks like:
While that may look a tinge confusing now, it’s a concept you’re already familiar with.
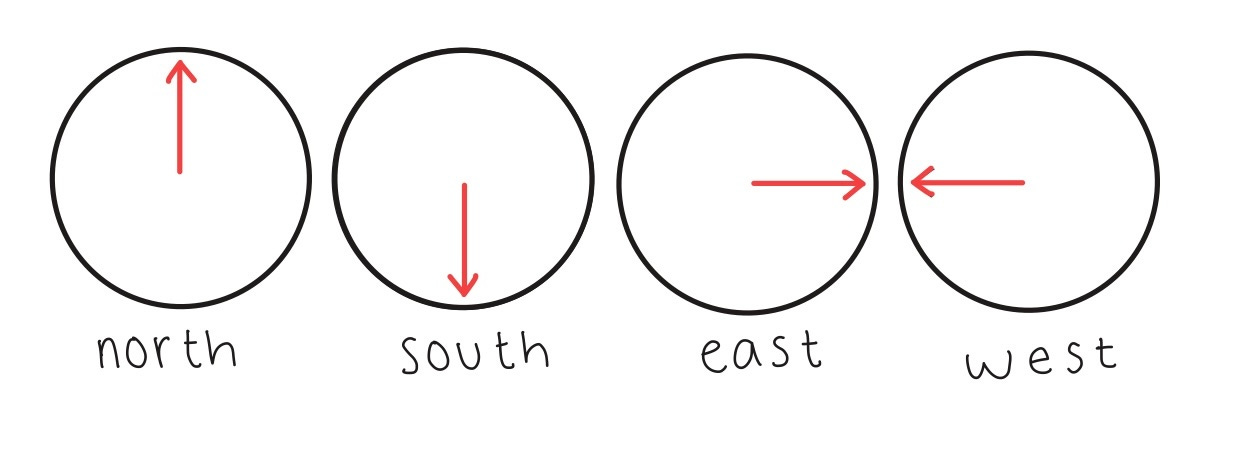
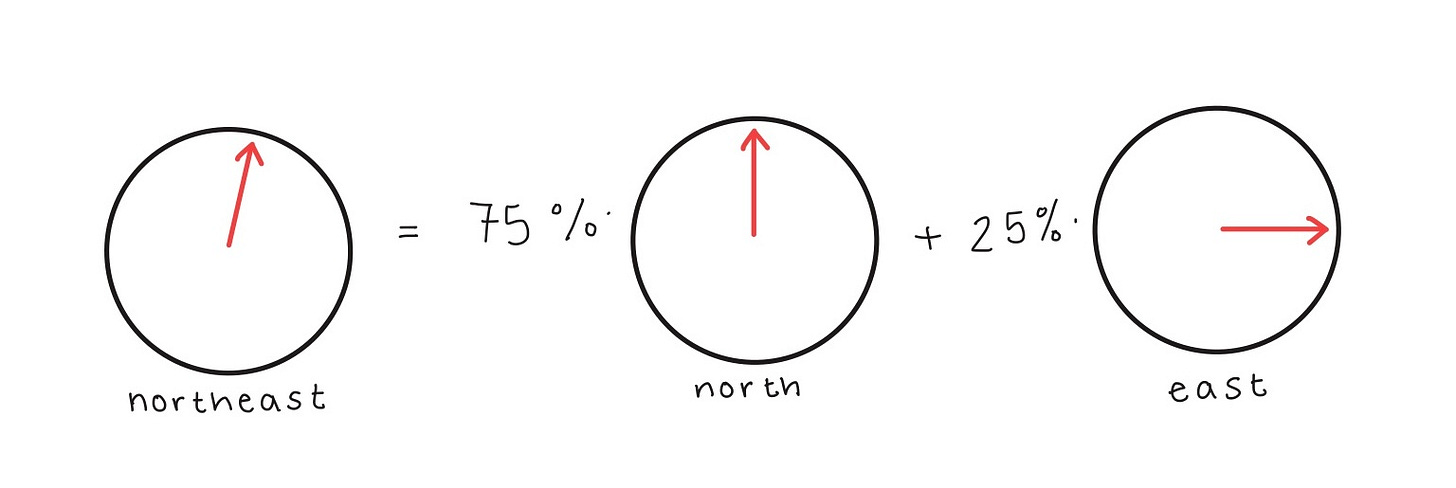
Think of linear combinations like a compass: by labeling four directions or “states,” we can get anywhere we want to go.
Here are our states:
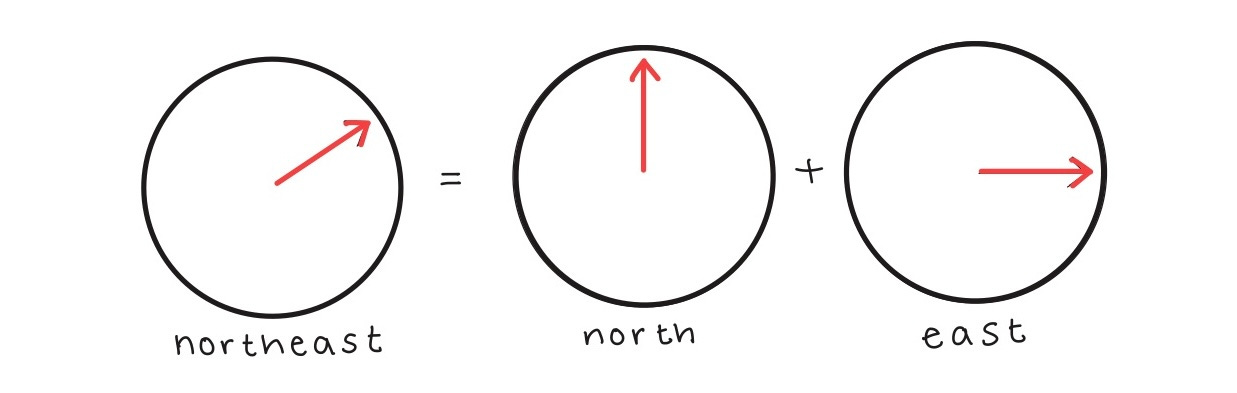
And here are some possible combinations:
If we wanted to get more specific, we could do so as well.
That’s what the little letters up front are for. If we replace them with percentages, we can know exactly how much more of one direction we need than the other.
Linear Combinations for Electrons
We can use the same idea for our electron’s energy states. Instead of considering our electron as one continuous release of energy, like a tennis ball, we can represent it as a combination of all the energy states it is likely to have.
Let’s call the total energy E and the energy states it can have E1, E2, and E3.
To take care of the randomness problem, we can simply follow the same approach as we did for the compass. We put a little percentage up front that lets us know how likely each energy value is.
Since those are constants and we don’t know what they are yet, we can call them a1, a2, and a3. They are also called Coefficients.
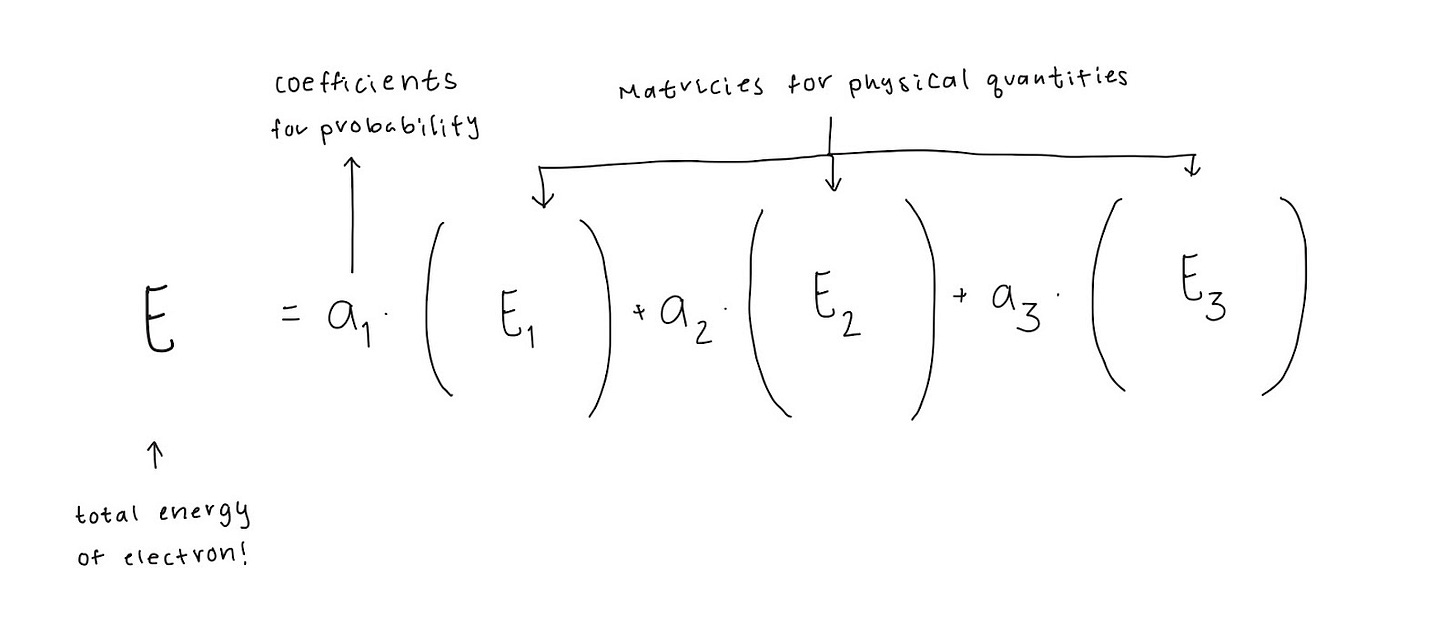
Finally, our electron needs to have discrete energy values. We need a mathematical tool that converts them into physical quantities, but allows us to count only specific numbers.
How about… Matrices?
Matrices are fancy tables that let us turn one set of numbers into another. They work to represent an electron’s energy states because only certain outcomes are allowed (which makes them discrete).
There’s a bit more to them, but that’s all you need for now.
Put it all together, and what do we get? An accurate representation of an electron!
The Best Part
Linear algebra is so important because it’s not just how we do quantum mechanics, but it is quantum mechanics.
What you might know as superposition is really just a linear combination of an electron’s energy states.
That’s also why it’s so important to learn the fundamentals of linear algebra if you want to dive into any of the subjects I mentioned at the beginning.
Machine learning, quantum mechanics, or computer science will become a lot easier once you know what they’re built on.
That’s because, just like in life, the answer to your problems usually isn’t in what you’re looking at, but how you’re thinking about them.
Alright, that’s enough philosophy from me. I’ve got science to do.
See you next time!
I want to thank Serena again for writing this valuable article!
Don’t forget to subscribe to The Quantum Notebook by Science with Serena.
Unlock access to every article on ‘Into Quantum’ by becoming a paid subscriber:




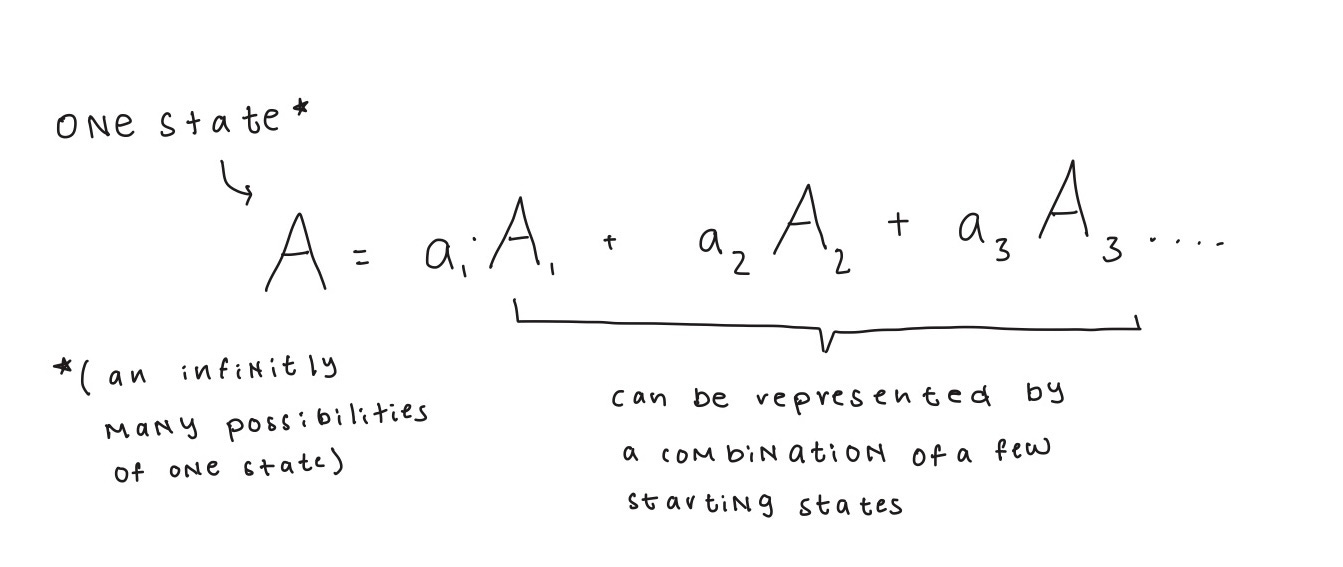
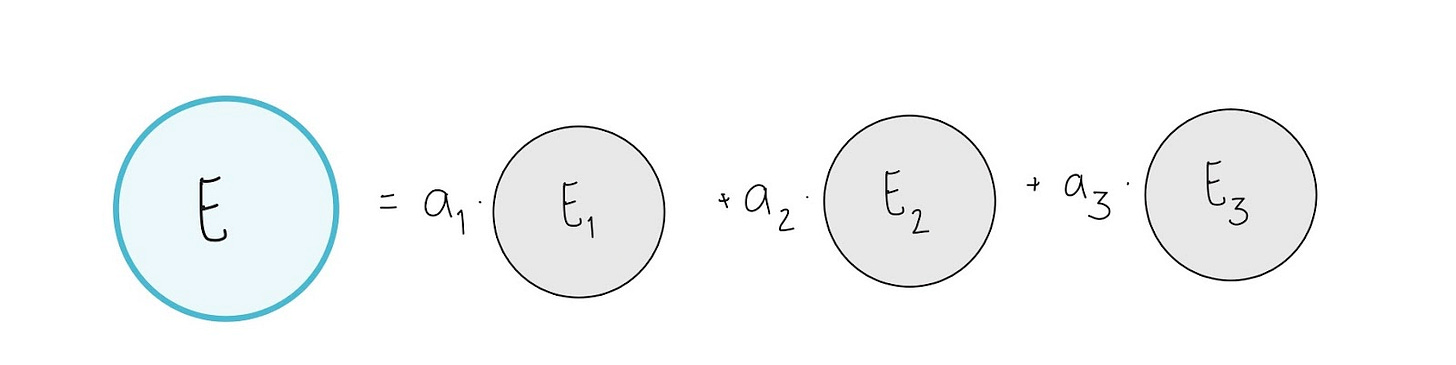


thanks for complete explanation , and beneficial information . looks like the article (linear algebra) is more important than it use to think .
Really good explanation! And complete with the (usual) eye catching figures